第６章　パソコンなどの「品質調整」

絶品フルーツモデルと似た状況が起きていた

　厚労省の2008年～2010年の生活扶助相当ＣＰＩの計算は実質的にパーシェ方式です。
この計算で絶品フルーツモデルに似た事態が現実に生じたことが極めて重要です。
価格指数が急落する一方で、計算上の購入数量が急拡大したのは、
テレビやパソコンなどのデジタル家電製品です。
まず、この当時のデジタル家電製品の価格指数の下落ぶりを図で示してみましょう。

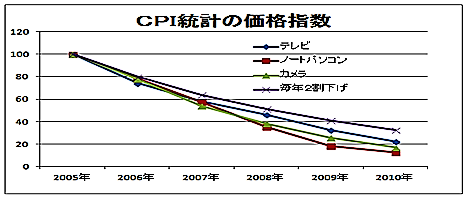
　総務省統計局のＣＰＩのサイトからデータを得ました。
テレビ、ノートパソコン、カメラの３品目の価格指数をグラフにしました。
一番上の線は、毎年２割という同じペースで価格指数が下がった場合の線形。
３品目の価格指数が毎年２割を超すようなペースで下がり続けた分かります。
生活扶助相当ＣＰＩの変化率へのデジタル家電製品の影響力は、
ラスパイレス方式のときに比べてパーシェ方式のときの方が圧倒的に大きくなりました。
しかも、パーシェ方式での計算値は｢計測誤差｣が目立つ状態になっています。
　ここが物価偽装問題では極めて重要なポイントです。
この計測誤差の原因をしっかり考えねばなりません。
　まず、先ほどの絶品フルーツのモデルを振り返ってみましょう。
2005年～2010年で価格が４分の１になった一方で、
絶品フルーツは１個→４個といった具合に数量が増えました。
この間ずっと１個だったのではないし、ずっと４個だったわけでもない。
１個から徐々に増えて４個になったわけです。
　しかし、ラスパイレス方式ではずっと１個だったという仮定、
パーシェ方式ではずっと４個だったという仮定で計算します。
現実に比べると、ラスパイレス方式の計算では絶品フルーツの影響が小さくなりすぎ、
パーシェ方式の計算では絶品フルーツの影響が大きくなりすぎ、と断定できます。
両方式の計算では、このような計測誤差はいつも生じます。
それとは別の特殊事情的な計測誤差が、厚労省の計算ではデジタル家電製品について生じました。
ここが重要なポイントです。ここをしっかり解明する必要があります。
デジタル家電製品でも、パソコンやカメラとテレビとでは事情が大きく異なります。
そこでまず、パソコンやカメラについて説明しましょう。
　2008年～2010年の生活扶助相当ＣＰＩの計算に焦点を当て、100万円ベース買い物かごで説明します。
2005年を基準時点とした総務省統計局方式と2010年を比較時点とした厚労省方式の買い物かごを比べます。
かごの中のノートパソコン、デスクトップパソコン、カメラの各年の代金は、次のグラフの通りです。
３品目のグラフとも、先に示した絶品フルーツモデルのグラフとよく似ています。
各品目とも①2005年と2010年の支出額割合に大きな差がない
②この５年間の価格指数は激落―といった状況が読み取れます。
こうした場合は、この５年間で計算上の購入数量が激増していることは先に説明した通りです。

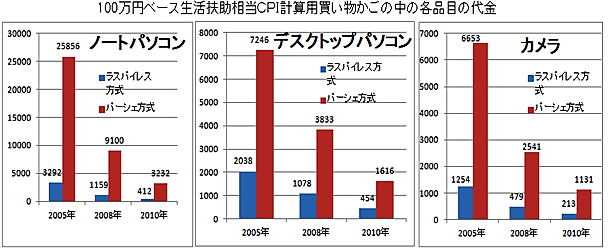
　2005年～2010年の購入数量の増加倍率は大きな数字。
ノートパソコンが7.9倍、デスクトップパソコンが3.6倍、カメラが5.3倍となっています。
ラスパイレス方式からパーシェ方式への切り替えで、
生活扶助相当ＣＰＩ変化率への影響力が、ほぼこの倍率だけ膨らんだことになります。
　「何だかおかしい」と思う人が多いはずです。
パソコンやカメラは2005年には既に一般家庭に相当に普及していたので、
2005年からの５年間で日本国民の平均的な購入数量がこんなに増えたとは到底思えないのです。
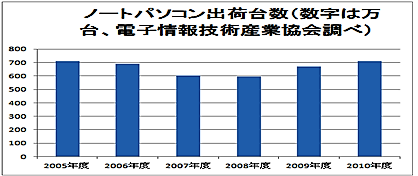
そこで、毎年の国内の出荷統計を見てみると、
やはり、パソコンやカメラの出荷台数はそれほど増えていません。
業界団体が公表しているノートパソコンの国内出荷統計の推移をグラフにしたのが次の図です。

物価指数計算に品質向上を反映させるのが品質調整

　このあたりの疑問を説明するカラクリが「品質調整」です。
物価指数の世界では、モデルチェンジが頻繁にあって性能向上が著しい品目について、
担当機関が｢品質調整｣という措置を取ります。
物価指数の対象品目が旧銘柄から新銘柄に変わって性能が大幅に向上。
しかし、販売価格はほとんど変わりがない。
こんな状況のときに、品質調整で大幅に価格指数を下げます。
｢お値打ちに買えるようになった｣といった感覚です。
この時期は、パソコンやカメラの性能向上が著しかったので、
パソコンやカメラについては品質調整が強力に実施されました。
価格指数激落の要因の大半は、品質調整だったのです。
現実には、パソコンやカメラは、小売価格や販売台数、支出額割合の動きは比較的おだやかでした。

「数量が増えたとみなす」決まりにも注意が必要

　｢品質調整したときは数量の扱いはどうなるのか｣という疑問も湧きます。
この点を考えるため、次の｢デジタル家電モデル｣を考えてみました。
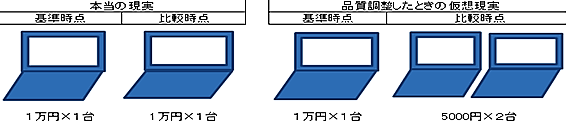
想定した条件は次の通りです。
①基準時点と比較時点の価格は１台１万円と同じ②購入台数も基準時点、比較時点とも１台で同じ
③モデルチェンジで性能が大幅に向上したので比較時点の価格指数は基準時点の半分になった
いつもの100万円ベース物価指数買い物かごでの計算上では、
デジタル家電１台の価格が１万円→5000円と下がったことになり、
比較時点の購入代金は「5000円×１台＝5000円｣となります。
しかし、このモデルの本当の現実では、比較時点の代金は１万円です。
モデルの中の現実と計算上の数字がずれてしまいました。
　こうした事態を防ぐため、品質調整をしたときは、
それに見合うよう｢数量が増えた｣とみなす作業をするのがルールです。
この場合は、数量が２倍に増えたとみなす。
すると、品質調整した仮想現実の世界では、
比較時点は｢5000円×２台｣の状態になって、代金は１万円となります。
本当の現実は、比較時点の代金は１万円なので、一応つじつまが合ったようです。
下の図を見て確かめてください。

　しかし、物価指数買い物かごの計算をするときに具合が悪くなります。次の図で確かめてください。
品質調整を実施した仮想現実の世界では、購入台数は基準時点が１台で、比較時点は２台です。
このため、購入台数はラスパイレス方式では基準時点、比較時点とも１台、
パーシェ方式では両時点とも２台として計算します。
その結果、デジタル家電の代金は、
ラスパイレス方式では１万円→5000円、パーシェ方式では２万円→１万円となります。

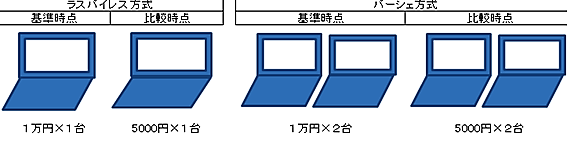
パーシェ方式のとき、基準時点の代金が｢１万円×２台｣で２万円になってしまうのが異様です。
モデルの中の本当の現実では、基準時点は購入台数が１台、購入代金は１万円なので、現実とずれます。
　品質調整をしたとき、パーシェ方式では｢数量が増えた｣扱いになります。
比較時点での｢数量が増えたとみなした数量｣で基準時点の計算もするわけです。
そのため、現実の基準時点の購入台数や購入代金とずれが生じてしまう理屈です。
　「基準時点の代金が過大になってデジタル家電代金の減少額も過大になり、
物価指数変化率への影響が大きくなりすぎる」という構図になるのです。
　先ほどの絶品フルーツのモデルでは現実に購入個数は増えましたが、
デジタル家電のモデルでは現実には購入台数は基準時点も比較時点も１台で同じで、
購入代金も基準時点、比較時点とも１万円で変わりがありません。
　そのため、基準時点～比較時点の代金減少額が１万円となり、いかにも過大に感じられます。
　デジタル家電モデルでは品質調整に絡んで、数字が現実と離れるよう二重の操作をしています。
価格は実際には変わっていないけれど、性能向上を反映させて価格指数が半分になったことにする。
その上、｢購入台数が２倍に増えたとみなす｣ということです。
　デジタル家電の購入者には、性能向上をそれほど意識していない人が多いとみられます。
そうした人にとっては、「性能向上分を数量の増加とみなす」といったパーシェ方式の計算は、
違和感が極めて強いはずです。

専門家の間では品質調整の過剰実施論が有力

　パソコンやカメラについての価格指数については、物価指数に詳しい専門家の間で、
「品質調整を強く実施しすぎてきたのではないか」といった懐疑的な意見が多いです。
ここも重要なポイントなので、じっくり検討しましょう。

この写真は、2017年10月31日号の週刊エコノミストに掲載された
永濱利行氏（第一生命経済研究所主席エコノミスト）の論文
「物価の基礎　『経済の体温計』とも呼ばれる経済政策を推進するための重要指標」の一部です。
ここにも、消費者物価指数の問題点としてパソコンやカメラの品質調整が挙げられ、
「利用者が活用しきれていない品質向上の分は、
需要側（利用者）からみれば架空の価格下落にすぎない」という解説があります。
　パソコンは、消費者物価指数統計の基準年が2000年になったときに、
消費者物価指数の対象品目になりました。
そのころからずっと、品質調整が過剰に実施されているという意見が多いのです。
じっくり考えてみると、それは当然に思えます。
　絶品フルーツの実際の価格が４分の１になって購入個数が４倍になれば、
「すごくおいしい果物が４倍買えた」という具合に現実に幸福感が増します。
一方、パソコンの性能向上が著しいとき、
実際の価格は変化がないが価格指数は「４分の１に下落した」とみなす品質調整を実施したときはどうか。
実際の購入台数は変わらないが、性能が向上しているので、購入台数が４倍に増えたとみなします。
ところが、メールのやりとりやホームページの閲覧といった単純な使い方が中心の人だと、
性能向上のありがたみはさっぱり感じません。
　絶品フルーツの購入個数が４倍に増えたときの幸福感の増大ぶりとはまったく違います。
　パソコンやカメラについての品質調整は、ヘドニックという方式で実施されています。
パソコンの場合は、ＨＤＤ記憶容量やメモリ容量、付属ソフトの有無などの性能と
商品価格との関係を重回帰分析という統計的手法で解析させたりし、ヘドニック方式で品質調整を実施しています。　
　次の画像は、内閣府経済社会総合研究所の所員や統計の専門家らが集まって２００４年６月に開かれた
「第１回基準改定課題検討委員会」の議事録の一部です。

　これを見ても、パソコンについてのヘドニック法が議論の的になっていることが分かります。
「パソコンを使うときにエクセルやワードしか使わない場合は、
いくら機能が増えても個人的な便益は増えない」という指摘があるだけでなく、
「ヘドニック法により品質向上が過大に評価されすぎていることを危惧している」という記述もあります。
　３つめの黒丸の部分の指摘も極めて重要です。
高齢者世帯の年金額では「物価スライド」という手法が使われていました。
その際の指標（デフレーター）として消費者物価指数が使われてきたことを念頭にした発言です。
平均的な高齢者世帯ではパソコンなどの性能向上を十分に生かした使い方はできていない。
そのため、パソコンなどについてヘドニック法で品質調整した消費者物価指数は、
下落率が大きくなりすぎたり上昇率が小さくなりすぎたりする。
だから、年金の物価スライドでは別の品質調整の手法を使うべきだという意見なのです。
　一般の高齢者世帯に比べて生活保護世帯では、パソコンの性能向上による恩恵はさらに小さいはずです。
パソコンのいろいろな機能を使いこなしている人の割合が生活保護世帯では一段と低いとみられるからです。
生活扶助相当ＣＰＩの下落率がヘドニック法による品質調整で過大になっていることは、
「生活保護世帯にはあまりにも厳しい」と筆者は考えます。
　消費者物価指数の計算構造についての日本銀行の研究蓄積は大きいです。
その日銀も、2013年１月２３日に公表した「『物価の安定』についての考え方に関する付属資料」
という重要文書の中でヘドニック法による品質調整の過剰実施論に言及しています。
３頁下の欄外の次の記述に注目ください。
　消費者物価指数の｢下方バイアス｣は、
消費者物価指数の変化率が現実に比べて低くなりすぎる現象を指した言葉です。

　下から５行目以下の部分が品質調整に関する指摘です。
パソコンを例示し、「パソコンの機能向上があってもすべての人がそれを使いこなすことが難しい現状では、
品質調整が時として過剰になる」といった説明をしています。

日本は海外諸国より品質調整を強く実施

　パソコンやカメラなどの品質調整をどの程度強く実施するかは、
世界各国の物価指数統計担当機関の考え方次第です。
そのため、世界各国でパソコンなどの品質調整の度合いに差が出ます。
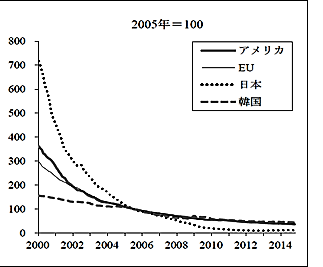
2015年に当時は駒澤大学経営学部教授だった熊倉正修氏が
「デフレと物価指数の品質調整」と題した論文の中で、この論点を説明しています。
熊倉氏は、パソコンなどの品質調整の度合いは日本が極めて強かったと指摘し、次の図も示しています。
各国のパソコンの価格指数（2005年＝100）を比較したものです。
日本の消費者物価指数のパソコン価格指数については、
ノートパソコンとデスクトップパソコンの価格指数を合成したものという意味の注釈がある。
この図では、日本でのパソコン価格指数の激落ぶりが目立ちます。
日本が他国よりパソコンの品質調整を強く実施したことは歴然としているように見えます。

価格指数が急落していれば購入数量は急増

　パソコンなどの品質調整の過剰実施論を踏まえ、さらに指摘しておきたいポイントがあります。
品質調整を強く実施すると、パソコンなどの価格指数下落率が大きくなるので、
消費者物価指数変化率を低くする影響が生じます。
その影響がパーシェ方式では、相乗的に一段と大きくなるのです。
　極めて重要なポイントです。例によってモデルで考えてみました。
想定した条件は次の(ア)（イ）（ウ）（エ）の通りです。
（ア）100万円ベース物価指数計算用買い物かごで考える
（イ）現実には基準時点にも比較時点にもデジタル家電を１台買った
（ウ）現実には１台当たりの購入価格は基準時点、比較時点とも１万円で変わらなかった
（支出額割合は基準時点、比較時点とも１％）
（エ）品質調整で価格指数は基準時点から比較時点にかけて大きく下がった
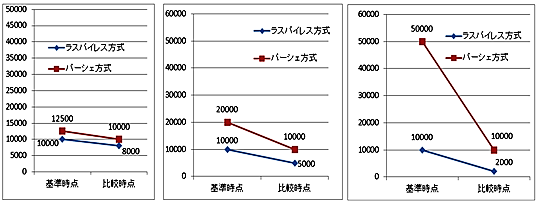
　基準時点→比較時点の価格指数の下落は「①100→80②100→50③100→20」の３パターンを想定しました。
品質調整した後の物価指数計算の想定の世界では、
１台当たりの購入価格は①では基準時点１万円→比較時点8000円、
②では基準時点１万円→比較時点5000円、
③では基準時点１万円→比較時点2000円、ということになります。
品質調整後の物価指数の計算上の世界では、
比較時点の購入台数は①では1.25台（比較時点の購入代金１万円を比較時点の単価8000円で割る）、
②では２台（10000円÷5000円）、③では５台（10000円÷2000円）ということになります。
基準時点→比較時点の価格指数と購入台数の推移をまとめると次の通り。
①100→80、１台→1.25台②100→50、１台→２台③100→20、１台→５台
品質調整を強く実施して価格指数を大きく下げるほど購入台数が増えることが分かります。
　ラスパイレス方式とパーシェ方式での計算結果を次のグラフで見てください。
価格指数の下落率が大きくなるほどパソコンの購入台数が増えるので、
パーシェ方式のときの代金減少額の膨らみ方が加速度的に大きくなります。
下落率が大きい場合は、両方式の計算結果が激しく乖離することが分かります。

　こういった現象はなぜ起きるでしょうか。
ラスパイレス方式からパーシェ方式に切り替えたときに計算上の購入数量が何倍に増えるかの計算式に当てはめると、
理解しやすいと思います。再掲した計算式を見てください。

今説明しているモデルでは、この式の後の分母分子のところは、分母も分子も１％なので１です。
そのため、（基準時点の価格指数÷比較時点の価格指数）がそのまま計算上の数量の増加倍率になります。
この割り算の答えは、価格指数の下落ぶりが激しいほど大きくなります。
数量増加倍率は、価格指数の推移が100→80のときは（100÷80）で1.25倍、
100→50のときは（100÷50）で２倍、100→20のときは（100÷20）で５倍という具合にどんどん大きくなります。
品質調整で価格指数が大きく下がった品目については
①価格指数の下落率が大きい②数量増加倍率の大きさが加速度的に大きくなる、
というダブル効果でパーシェ方式に切り替えたときの影響が異様なほど大きくなるのです。
　もう一つ理解しておきたいポイントがあります。
2005年～2010年当時は、パソコンやカメラの価格指数は品質調整の影響で毎年、大幅下落が続き、
前年比下落率は２～３割の状態が続きました。
この状態では、基準時点から比較時点までの経過期間が長いと、
パーシェ方式で計算したときに品質調整の影響が激烈な形で現れるのです。
　カラクリは難しくありません。デジタル家電という項目があったと仮定しましょう。
基準時点は2005年。現実には、その年から毎年ずっと１台１万円のデジタル家電を１台買っていたとします。
しかし、品質調整によって価格指数は毎年20％ずつ下落したとする。
価格指数は2005年＝100、2006年＝80、2007年＝64…という具合に小さくなります。
　一方、計算上の各年の購入台数は「１台×（2005年の価格指数／各年の価格指数）」ではじき出せます。
計算上の購入個数は、2005年が１台、2006年が1.25台、2007年が1.5625台、2008年が1.953125台…と増えていきます。
2005年からの経過年数が長いほど購入台数が増えるわけです。

トップページに戻る