第５章　方式変更で電気製品の影響が極大化

　この章では、計算方式の問題に絞って分析していきます。
これまでの説明で、厚労省が異例の計算方式を使ったことは明らかにしました。
　しかし、「異例の方式を使うといつも物価指数の下落率が大きく膨らむ」わけではありません
異例である「実質的なパーシェ方式」を使ったときに下落率を膨らませる状況があったのです。
それがどういう状況なのかをじっくり説明していきます。

各項目の価格指数の変わり方はどうだったか

　日常の買い物を思い浮かべながら、物価指数計算の基本的な仕組みを振り返ってください。
買い物かごに入っている品目の合計代金の変化率が物価指数の変化率です。
基準時点と比較時点の買い物かご合計代金を比べます。
各品目の代金の変化率は、各品目の価格の変化率に連動します。
　例えば、Ａ品目の価格が基準時点〜比較時点で２倍になったのであれば、
Ａ品目の比較時点の代金は、基準時点の代金の２倍になります。
　買い物かごの中の各品目の価格が、基準時点〜比較時点であまり変わらなければどうでしょう。
各品目の代金はあまり変わらないので、買い物かごの合計代金にも大きな変化は出ません。
物価指数の変化率も小さくなります。
　代金の変化率がそれなりに大きい品目があるから、物価もそれなりに変化するわけです。
各品目の代金の変化率は、各品目の価格の変化率に等しいので、
結局、各品目の価格変化率が大きいかどうかをしっかり見る必要があるのです。
　前置きが長くなりました。そういう事情で、各品目の価格変化率のデータを見ましょう。
ここで見るのは、2010年を100とした2008年の価格指数です。
厚労省が2008年生活扶助相当ＣＰＩを計算する際に対象にした268項目を見ます。
2010年を100とした2008年の価格指数は、
「2008年の価格は2010年の価格の何倍だったか」の倍率に100を掛けた数字です。
筆者の分析内容を整理した下の表を見てください。

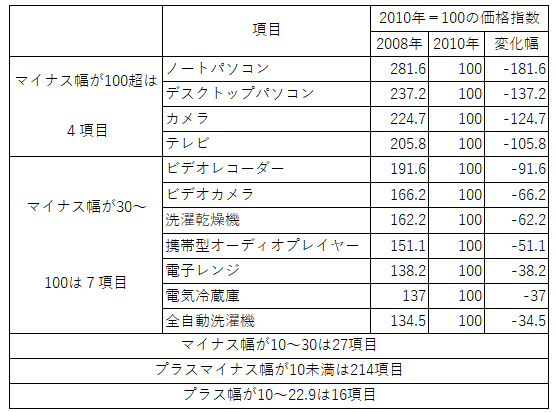
　各項目の2008年〜2010年の価格指数の変化幅の大きさでランク分けしています。
まず、表の下から２段目に注目してください。
価格指数の変化幅が10未満の項目が214項目もあります。全体の約8割の項目数です。
価格指数がプラスの場合、マイナスの場合の両方を含めています。
　価格の変化が小さかった項目が大半だったということです。
物価安定が続いていたことの表れでもあります。
　次に、一番下の段を見てください。価格指数が著しく上昇した項目が皆無ということです。
この２年間で、価格指数が一番上がったケースでも「77.1→100」なのです。
　続いて、下から三番目の段を見てください。
価格指数のマイナス幅が10〜30の項目数は27です。それなりに多く、物価は全体に下落基調です。
　この表で非常に目立つのは、電気製品が並んでいる上の方の部分です。
　物価指数の下落幅が100を超す項目が４つあります。
ノートパソコン、デスクトップパソコン、カメラ、テレビです。
価格指数のこの激落ぶりは通常の項目ではありえません。
この４項目は、それぞれ深い事情がある「わけあり項目」なのです。
その事情によって、実質的なパーシェ方式で計算されたときに、
物価指数変化率への影響が非常に大きくなりました。それぞれの事情は、後で詳しく説明します。
　価格指数の変化幅が30〜100の項目数は７です。すべてが電気製品であることに注目ください。

物価指数変化率への影響が大きい項目の特徴は？

　各項目が物価指数変化率にどれだけ影響したかは「寄与度」としてきっちり把握できます。
これは物価指数計算のいいところです。それでは、寄与度の大きさは何で決まるのでしょうか。
　第２章で、寄与度の決まり方も少し説明しました。
日常の買い物の場面や、物価価指数計算用の買い物かごを思い浮かべながら読んでください。
単純に「支出額割合の大きな項目の価格が大きく動くと、物価指数への影響が大きい」と言えます。
日常の買い物の感覚とぴったり合います。
　基準時点〜比較時点の物価指数変化率を計算するときのある項目の寄与度は、
その項目の代金増減額を基準時点の合計代金額で割れば得られます。
　どんな場合に代金の増減額が大きな数字になるのでしょうか。
基準時点の代金が大きい項目で、価格変化率が大きかったときに増減額は大きくなります。
基準時点の代金が大きい項目は、基準時点で支出額割合が大きい項目とイコールです。
　ここまでは分かりやすいのですが、ここから若干難しい感じになります。申し訳ありません。
　まず、ラスパイレス方式です。正確に言えば、基準時加重相対法算式です。
この場合は、各項目の基準時点の支出額割合と価格変化率のデータがあります。
このデータを使って寄与度（単位はポイント）を求める式は次の通りです。

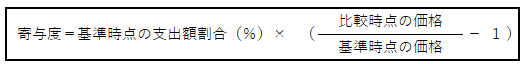
　意外にシンプルな式です。意味合いも分かりやすい式です。
％表示の支出額割合の数字に「比較時点の価格／基準時点の価格ー１」を掛ければＯＫです。
「比較時点の価格／基準時点の価格ー１」は、価格の上昇率または下落率です。
つまり、価格の変化率。寄与度は、基準時点の支出額割合（％）に価格の変化率を掛ければ出せるのです。
　この式から、基準時点の支出額割合が大きいほど、
また、価格の上昇率や下落率が大きいほど、寄与度の絶対値が大きくなることが分かります。
寄与度は、プラスの場合とマイナスの場合の両方があるので、
「寄与度の絶対値が大きくなる」という表現が正確です。
　この式の価格の変化率の部分を取り出して考えてみましょう。興味深いポイントがあります。

　上の式を見て確認してください。
値下がりした場合、つまり比較時点の価格の方が安いときは、この部分はマイナスになります。
値下がりしたのだから当然です。ただ、この部分はマイナス１よりは小さくなりません。
　例えば、基準時点に100円だった価格が比較時点に１円にまで激落したとしましょう。
この部分は「100分の１−１」でマイナス0.99になります。
価格が安くなった場合の影響は限定的なのです。
　値上がりした場合は、この部分はプラスになります。
そして、価格が急上昇した場合の影響は限定的ではありません。
例えば、基準時点に30円だった価格が比較時点に120円になったらどうか。
この部分は「30分の120−１」でプラス３という大きな数字になってしまいます。
　しかし、先ほど確認したように、
生活扶助相当ＣＰＩの2008年〜2010年の計算では、価格が猛烈に急上昇した品目は皆無でした。
プラスの寄与度が目立って大きいといった項目はなかったのです。
　次はパーシェ方式。正確に言えば、比較時加重相対法算式です。
厚労省が2008年〜2010年の生活扶助相当ＣＰＩを計算したときのように、
「比較時の物価指数が100、基準時の物価指数は100でない」という形で考えます。
各項目の比較時の支出額割合と基準時〜比較時の価格変化率のデータがあります。
この場合の寄与度の計算式は次の通りです。

　この式の最後の部分にある「100／基準時点の物価指数」は１に近い数字なので、あまり影響しません。
式の最初の部分から、比較時点の支出額割合が高いほど、
寄与度の絶対値が大きくなることが読み取れます。これも常識的な話です。
問題は価格の変化率の部分です。ここが非常に興味深い。そこだけ抜き出したのが次の式です。

　値上がりした場合、つまり比較時点の価格の方が高いときは、この部分はプラスになります。
値上がりしたのだから当然です。ただ、この部分はプラス１よりは大きくなりません。
　例えば、基準時点に１円だった価格が比較時点に100円にまで急上昇したとしましょう。
この部分は「１−100分の１」でプラス0.99になります。
価格が高くなった場合の影響は限定的なのです。
　一方、値下がりした場合、つまり価格が安くなったときは、この部分はマイナスになります。
そして、価格が激落した場合の影響は限定的ではありません。
例えば、基準時点に120円だった価格が比較時点に30円になったらどうか。
この部分は「１−30分の120分」でマイナス３というマイナスの大きな大きな数字になります。
　先ほど確認したように、生活扶助相当ＣＰＩの2008年〜2010年の計算では、
価格が激落した品目グループがありました。テレビやパソコンなどの電気製品です。

「100万円ベース買い物かご」で個別品目の影響が明瞭に

　第３章で「100万円ベース買い物かご」を紹介しました。個別品目の影響を明瞭に示す工夫です。
　ここでは、生活扶助相当ＣＰＩの計算を100万円ベース買い物かごで示す手順を説明します。
厚労省は2010年〜2011年の計算では、517の個別品目を300項目にくくり直して計算しました。
300項目のウエイト合計は6393です。下の計算表のＢ列を見てください。
Ｂ列の各項目の数字は「6393分のいくつ」の6393分比です。
この数字を１万分比の数字に変えます。
　Ｂ列の各項目の数字に「6393分の10000」を掛ければＯＫです。
こうして出てきた１万分比のウエイトの数字をＣ列に並べます。
各項目のＣ列の数字にＤ列の数字（すべて100）を掛けると、各項目の2010年の代金になります。
それがＦ列の数字で、合計が100万円になります。
　次に、各項目のＣ列の数字にＥ列の数字（2010年を100とした2011年の価格指数）を掛けます。
その積の数字がＧ列の数字。各項目の2011年の代金です。合計は99万4796円です。
　Ｇ列の数字からＦ列の数字を差し引くと、各項目の増減額になります。Ｈ列に並べておきます。
Ｈ列の数字を2010年の買い物かご合計代金の100万円で割って100を掛けたのが寄与度（Ｉ列）です。

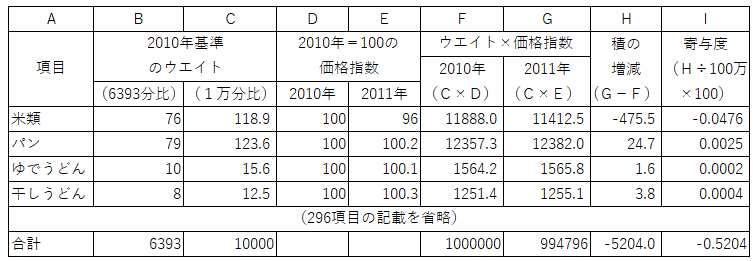
2010年〜2011年の厚労省計算の買い物かご

　この期間は、厚労省も通常の基準時加重相対法算式（ラスパイレス方式）で計算しています。
総務省統計局と同じ方式とも言えます。買い物かごの図をじっくり見てください。

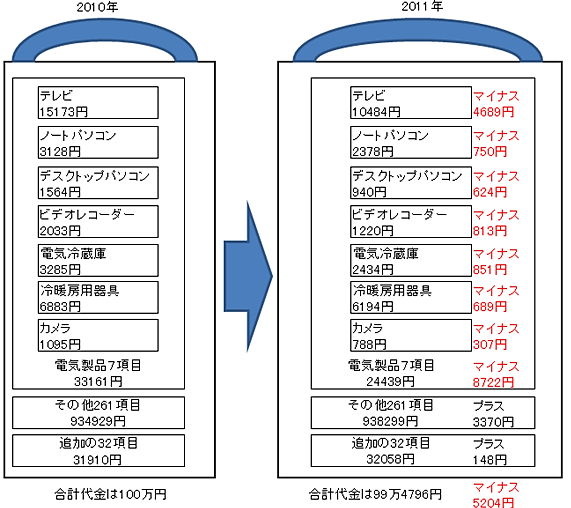
通常の計算方式を使っていても、電気製品の影響が非常に大きいのが目を引きます。
2010年の各項目の代金が一般世帯平均の支出額割合で設定されているからです。

異常さが浮き彫り！2008年〜2010年の厚労省計算の買い物かご

　続いて、厚労省の2008年〜2010年の計算の100万円ベース買い物かごを見てください。

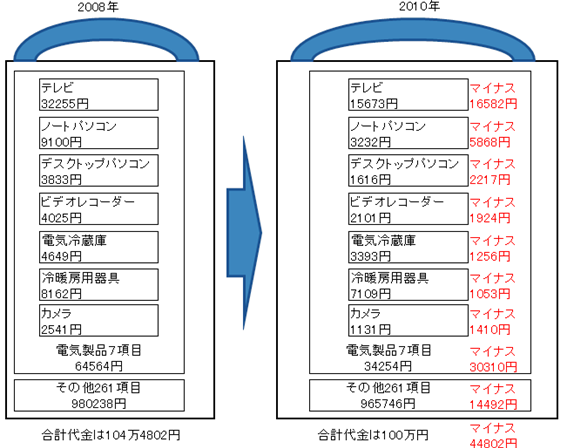
　テレビやパソコンなどの影響が猛烈に大きく、驚嘆される人が多いはずです。
一人暮らしの生活保護利用者の年間の生活扶助費は、100万円弱です。
2008年については、その中からテレビに32255円も支出したことになっています。
2010年は15673円なので、テレビ代金は２年で16582円も減ったことになっています。
　電気製品７品目の代金は、2008年64564円→2010年34254円で、30310円の減少。
一人暮らしの生活保護利用者の年間の生活扶助費は概ね100万円弱です。
平均的な生活保護世帯が電気製品にこんなに支出することはありえません。
　というか、平均的な一般世帯でも電気製品にこんなに支出しません。
2008年〜2010年の生活扶助相当ＣＰＩを計算するときの対象品目は485。
現実には、一般世帯でもこの485品目の中のテレビの支出額割合は2010年の1.57％が突出して高いのです。
　厚労省の生活扶助相当ＣＰＩの計算上の世界では、とんでもないことが起きました。
485品目中のテレビの支出額割合が2008年に3.09％まで跳ね上がったのです。
　こうした異様に見える厚労省の計算が、生活扶助費の大幅削減に直結しました。
このあたりのカラクリを是が非でも解明しなければならないわけです。

統計局方式で計算してみた2008年〜2010年の買い物かご

　総務省統計局の通常のラスパイレス方式で2008年〜2010年の生活扶助相当ＣＰＩを計算した場合は、
2005年が基準年で、2008年や2010年が比較年になる。
電気製品７項目を中心に「100万円ベース買い物かご」にして説明しようとしたのが次の図である。

2008年〜2010年の各項目の増減額を見ると、合計代金の減少額は18031円である。
電気製品７項目の減少額が合計で4507円、その他261項目の減少額は合計で13524円であることが分かる。
この時期は、原油価格下落の影響などがあって相当多くの品目の価格指数が少しずつ下がった。
電気製品の価格指数低下の影響ばかりが目立つという状況ではなかったわけだ。

電気製品の影響の異常な大きさを寄与度でも確認

　2008年〜2010年の生活扶助相当ＣＰＩ変化率は、厚労省方式と総務省統計局方式で大違いです。
どの項目の影響でそうなるかは、各項目の寄与度で厳密につかめます。
そこで、筆者が100万円ベース買い物かごの計算に手を加えて寄与度を計算しました。
その結果を表まとめたので、じっくり見てください。

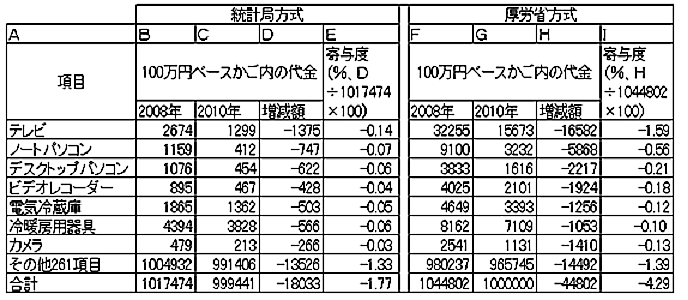
　左側の統計局方式では、生活扶助相当ＣＰＩの変化率はマイナス1.77％。
テレビとパソコンのマイナスの寄与度は合計でも0.27ポイントに過ぎないので、
テレビやパソコンの影響はそれほど大きくありません。
ところが、右側の厚労省方式では、生活扶助相当ＣＰＩ変化率はマイナス4.29％。
下落率が一気に膨らみます。ここが異常であり、物価偽装の核心部分です。
マイナスの寄与度はテレビが1.59ポイント、パソコンが0.77ポイントなので、
テレビやパソコンの影響が決定的に大きいと言えます。
　なぜ、そういった現象が起きたのか、じっくり検討しましょう。

パーシェ方式の計算では数量増加の倍率の分だけ影響度が膨らむ

　物価指数の変化率は、ラスパイレス方式とパーシェ方式による計算値が大きくずれる場合があります。
その代表が｢価格が激落する一方で購入数量が激増する｣といった品目グループがあるときです。
　物価指数計算用買い物かごの中に｢絶品フルーツ｣があるというモデルで考えてみましょう。
１個当たりの価格は、2005年が4000円、2008年が2000円、2010年は1000円と仮定します。
抜群においしい果物の価格が４分の１に激落したので、購入数量が激増したという想定です。
購入個数は、2005年１個、2008年２個、2010年４個とします。
代金は、2005年が｢4000円×１個＝4000円｣、2008年が｢2000円×２個＝4000円｣、
2010年は｢1000円×４個＝4000円｣で、各年とも4000円です。

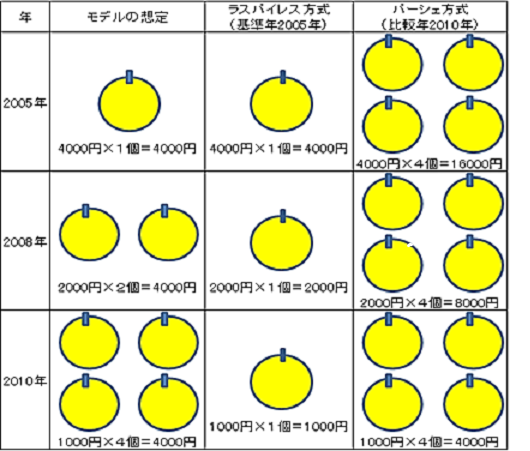
　上の図をゆっくり眺めてください。
ラスパイレス方式では、基準時点の個数が比較時点にも同じとして計算します。
そのため、2005年を基準年にしたラスパイレス方式での計算上の代金は、2005年が｢4000円×１個＝4000円｣、
2008年が｢2000円×１個＝2000円｣、2010年は｢1000円×１個＝1000円｣となります。
　一方、パーシェ方式では、比較時点の個数が基準時点にも同じとして計算します。
するので、2010年を比較年にしたパーシェ方式での計算上の代金は、2005年が｢4000円×４個＝16000円｣、
2008年が｢2000円×４個＝8000円｣、2010年は｢1000円×４個＝4000円｣となります。
　現実の絶品フルーツ代金は、モデルの想定では各年とも4000円。
しかし、物価指数の計算上の代金の推移は、ラスパイレス方式では4000円→2000円→1000円。
パーシェ方式では16000円→8000円→4000円です。
各年の代金額は、パーシェ方式で計算した場合の方が４倍大きいことに注目ください。
絶品フルーツの購入数量が、2005年→2010年で４倍に増えたので、
比較年の2010年の購入数量で計算するパーシェ方式の方が物価変動率への影響力が４倍大きくなる理屈なのです。

数量を計算に使っていないのに「数量増加の倍率」がつかめる

　多くの国の現在の消費者物価指数の計算では、数量は使いません。
そのため、ラスパイレスからパーシェに計算方式を切り替えたとき、
物価指数変動率への個々の品目の影響力がどう変わるかの筋道がつかみにくい感じです。しかし、心配御無用。
数量の数字は表面には出ていなくても、基準時点〜比較時点で｢購入数量が何倍に増えたか｣はつかめるのです。
　各品目の代金に｢代金＝単価×購入数量｣という式が成り立っているからです。
ある品目の基準時点と比較時点の価格指数、基準時点と比較時点の支出額割合がともに分かっているときは、
基準時点から比較時点にかけて各品目の数量が何倍になったかが簡単な計算式で示せます。
表面には出ていない「計算上の倍率」を求める式です。




トップページに戻る