�����U��
�g�b�v�y�[�W�ɖ߂�
��R�́@���v�ǂ͐��E�W���̕����Ōv�Z
�@����ҕ����w���́A���ɏd�v�ȓ��v�Ȃ̂ŁA����������Ɍv�Z����Ă͍���܂��B�@
����́A���E�̂ǂ��̍��ł������ł��B�����ŁA���ۓI�ȃ}�j���A��������Ă��܂��B
���s��2004�N�B�^�C�g���́u����ҕ����w���}�j���A���@���_�Ǝ��H�v�B
�h�k�n�i���ۘJ���@�ցj��h�l�e�i���ےʉ݊���j�ȂǂU�̍��ۋ@�ւ����͂����Y���ł��B
���{��̖�{��2005�N�ɏo�ł���Ă��܂��B�ʐ^���������������B900�ŋ߂������镪�����{�ł��B
���e�͑����ɓ���ł����A�M�҂͈ꐶ�����ɉ�ǂ��悤�Ƃ��Ă��܂��B
�@���{�ł́A����ҕ����w���̒S���͑����ȓ��v�ǁB
�M�҂̈�ۂł́A���v�ǂ̓}�j���A���ɂ҂����艈���ď���ҕ����w���̋Ɩ����s���Ă��܂��B

�v�Z���@�̐�����v�Z�Ɏg���f�[�^�Ȃǂ̏����J�͏[��
�@����ҕ����w�����w�Ԃɂ́A�����ȓ��v�ǂ̂b�o�h�̃z�[���y�[�W�ɐe���ނ��Ƃ��厖�ł��B
����ҕ����w���Ɋւ���f�[�^�����ځB����ҕ����w���̌v�Z���@�Ȃǂ���������Ă��܂��B
�u�b�o�h�v�̃L�[���[�h�Ō�������A�g�b�v�y�[�W�ɓ���܂��B���̉摜������ł��B
�@����ɂ���u���v�̊T�v�v�̕������N���b�N�B�u����ҕ����w���̂����݂ƌ����v�̃y�[�W���o�Ă��܂��B
���ꂪ�厖�ȕ��ޗ��ł��B������d���Ζ@�Z���̊�{�I�ȍl��������������Ă��܂��B

�v�Z�Ɏg���f�[�^�͊e�i�ڂ̃E�G�C�g�Ɖ��i�w��
�@�����ȓ��v�ǂ�����ҕ����w�����v�Z����ۂɂǂ�ȃf�[�^���g���Ă��邩�m�F���܂��傤�B
�e�i�ڂ̎x�o�z�����i�E�G�C�g�j�Ɖ��i�w���ł��B
�@���̉摜�́A���v�ǂb�o�h�T�C�g�Ɍf�ڂ���Ă���f�[�^�ł��B
�U�i�ڂɊe�i�ڂ�2015�N��̃E�G�C�g�̐���������܂��B
���v�ǂ́u�P�����̂����v�̂P������Ŋe�i�ڂ̃E�G�C�g�������Ă��܂��B
�@�Ⴆ�A�U�i�ڂ̂d��ɂ́u�ėށv��62�Ƃ�������������܂��B
�@�b�o�h���v�̑ΏۑS�i�ڂ̍��v�̃E�G�C�g��1���B���̒��ŕėނ̃E�G�C�g��62�B
�ėނ̎x�o�z�����͂P������62�ł���A���\���ł�0.62���Ƃ������ƂɂȂ�܂��B
���v�ǂ����{����ƌv�����ł́A�Ώې��тɕi�ڕʂ̎x�o�z���q�˂܂��B
���̌��ʂ̐��������Ƃɓ��v�ǂ��b�o�h���v�̊e�i�ڂ̃E�G�C�g��ݒ肷��̂ł��B
2015�N��̃E�G�C�g�́A2015�N�̉ƌv���������ƂɂȂ��Ă��܂��B
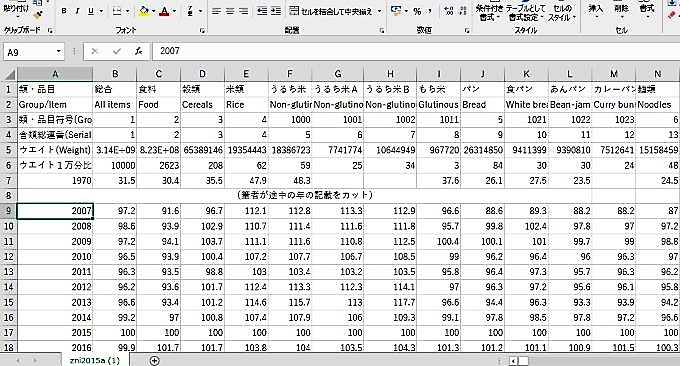
�@���̉摜�̂V�i�ڂ���́A�e�i�ڂ̔N���ς̉��i�w���̃f�[�^�ł��B
���v�ǂ́A�����������v�����Ŋe�i�ڂ̏������i�̐��ڂׂĂ��܂��B
��������Ƃɓ��v�ǂ��e�i�ڂ̉��i�w����ݒ肵�Ă��܂��B
2016�N�`2020�N�̉��i�w���́A2015�N��100�Ƃ����������g���܂��B
�@�d���18�i�ڂɕėނ̉��i�w����103.8�Ƃ�������������܂��B
2015�N�`2016�N�ŕėނ̉��i��1.038�{�ɂȂ������Ƃ������܂��B���̔{����100�{�����i�w���ł��B
103.8�Ƃ�����������͕ėމ��i��3.8���㏸�Ƃ����������ǂݎ��₷���ł��B
�Ώەi�ڂȂǂ��T�N���ƂɌ����������
�@�����ȓ��v�ǂ������̏���ҕ����w�������\���Ă��܂��B�N���ς̏���ҕ����w�������\���܂��B
���v�ǂ́A����_�𢐼���5�Ŋ�����N��ƔN�P�ʂɂ��Ă��邽�߁A���N��ƌĂ�ł��܂��B
��N��2000�N�A2005�N�A2010�N�A2015�N�c�Ƃ�����ł��B
�����I�ɂ́A2006�N�`2010�N��2005�N����N�ɁA2011�N�`2015�N��2010�N����N�ɂ��Čv�Z���܂��B
����ҕ����w�����v�Z����Ƃ��̑Ώەi�ڂ́A600�߂�����܂��B
�����āA5�N���Ƃ̊����̂Ƃ��ɁA�i�ڂ����ւ��܂��B
���܂蔃���Ȃ��Ȃ����i�ڂ́A�v�Z�Ώۂ���O���A�����l�������Ă����i�ڂ��v�Z�ΏۂɊ܂߂܂��B
2005�N��̔�������������2010�N��̔����������ɕς���C���[�W�́A�}�ɂ���Ƃ���Ȋ����ł��B
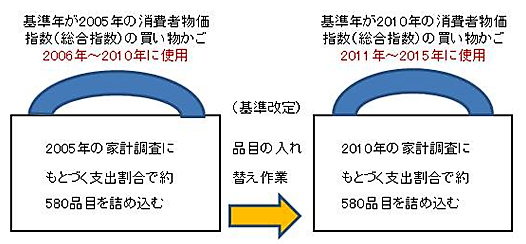
�u�ڑ��v�Ƃ�����@�Ōp�������m��
�@�����ȓ��v�ǂ̏���ҕ����w���̌v�Z���[���ł́A5�N���Ƃɔ����������̒��g���ς��܂��B
���̂��߁A�A�������S�z�ɂȂ�܂��B
�@�Ⴆ�A2006�N�`2010�N�́A�v�Z�̌��ʏo�Ă���CPI��2005�N��100��2005�N��̐����ł�.
����A2011�N�`2015�N�̂b�o�h��2010�N��100��2010�N��̐����ł��B
2008�N�̂b�o�h��2005�N��100�̐����ł���A2011�N�̂b�o�h��2010�N��100�̐����ƂȂ�܂��B
���̂Q�̔N�̂b�o�h�́A���ڂɂ͔�ׂ��܂���B
�@���̖�����������̂���ڑ���Ƃ�����@�ł��B
�b�o�h���v�̑S�i�ڂ��Ώۂ̂b�o�h�����w���̌����̓��������Ƃɍl���Ă݂܂��傤�B
���̐}��O���t���������茩�Ă��������B
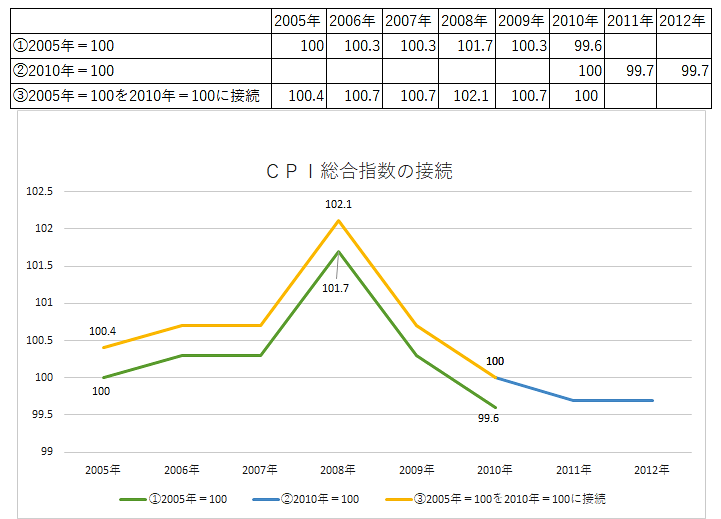
�@2006�N�`2010�N�̂b�o�h�����w���́A2005�N��100�̐����Ƃ��ďo�܂��B�\�̇@�̒i�̐����ł��B
100��100.3��100.3��101.7��100.3��99.6�Ƃ������ڂł��B
2011�N�ȍ~��2010�N��100�̂b�o�h�����w���ɂȂ�܂��B���ꂪ�A�̒i�B100��99.7��99.7�Ƃ��������ł��B
�@�O���t�̒ʂ�A2005�N��100�̇@�̒i�̗̐���2010�N��100�̇A�̒i�̐̐��͂���Ă��܂��B
�@�̐����2005�N��100��2008�N��101.7�ƁA�A�̐����2010�N��100��2011�N��99.7�͔�ׂ��܂���B
�@�������悤�ł����A��D�̑ŊJ����̂ł��B
100��100.3��100.3��101.7��100.3��99.6�Ƃ������ځB
����͊e�N�̕����w�����u100�F100�D3�F100.3�F101.7�F100.3�F99.6�v�Ƃ�����ł��邱�Ƃ������܂��B
���̔�̓��e��ς����ɁA�Ō��2010�N�̐�����100�ɂ���A�������܂��B
99.6��100�ɂ���ɂ́A99.6����100���|���܂��B
�@�̒i�̐����̂��ׂĂ�99.6����100�i�ق�1.004�j���|����A
�B�̒i��100.4��100.7��100.7��102.1��100.7��100�ɂȂ�̂ł��B
�u100:100.3:100.3:101.7:100.3:99.6��100.4�F100.7�F100.7�F102.1�F100.7�F100�v�B
���ӂ̔�̓C�R�[���ɂȂ��Ă���̂ł��B
�@�O���t�Ō���ʂ�A�B�̉��F�̐��͇A�̐̐��Ɍ����ɐڑ����܂����B
����ŁA�B�̐����2008�N��102.1�ƇA�̐����2011�N��99.7�ڔ�ׂ��܂��B
��������2.35���B�ڑ��Ƃ�����@�́A����������̊ȒP�Ȃ��̂ł��B
�����w���́u���i�w���̉��d���ρv�Ƃ��ĊȒP�Ɍv�Z�ł���
�@����ҕ����w���̌v�Z�́A�G�N�Z���̕\�v�Z���ł���l�Ȃ�������܂���B
�����ȓ��v�ǂ��g���Ă��������d���Ζ@�Z���̏ꍇ�́A���̗v�̂ł��B
�܂��A�e�i�ڂ��ƂɁu����_�̃E�G�C�g�~����_��100�Ƃ�����r���_�̉��i�w���v���v�Z�B
���ɁA�E�G�C�g�~���i�w���̐ς̍��v������_�̃E�G�C�g�̍��v�Ŋ���܂��B
���ꂾ���ŁA��r���_�̕����w���i����_��100�j���o�Ă��܂��B
�@2018�N9���̂b�o�h�����w�����v�Z����T���̎菇�́A���̒ʂ�ł��B
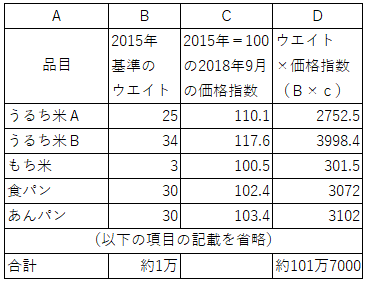
�@2015�N����N�Ȃ̂ŁA�v�Z�Ɏg���e�i�ڂ̃E�G�C�g��2015�N��̃E�G�C�g�ł��B
�e�i�ڂ̉��i�w���́A2015�N��100�Ƃ��������ɂȂ�܂��B
2018�N9���̂b�o�h�����w���i2015�N��100�j�́A
�c��̍��v��1017000���a��̍��v�̂P���Ŋ�����101.7�ɂȂ�܂��B
�i���Ӂ����̕\�̍��v���̐����͊T���ɂ��Ă���܂��j
�@���̌v�Z�́u�e�i�ڂ̃E�G�C�g���d�݂ɂ����e�i�ڂ̉��i�w���̉��d���ρv�ɂȂ��Ă��܂��B
�����͑����̕i�ڂ̉��i�̕��ϓI�ȓ����������w�W�B�u���i�w���̉��d���ρv�ł���A�����ɍ��������ł��B
������d���Ζ@�Z����100�{�����v�Z
�@���v�ǂ́A����ҕ����w�������X�p�C���X�����̕ό`�ł��������d���Ζ@�Z���Ōv�Z���Ă��܂��B
�u���i�w���̉��d���ςƊ�����d���Ζ@�Z���̊W�͂ǂ��Ȃv�Ƌ^������l������͂��ł��B
�����ŁA��Q�͂ł悭�o�ꂵ���~�J���E�����S�����w�����f���ōl���Ă݂܂��B
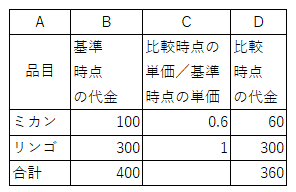
�@���̕\�̌v�Z�́A������d���Ζ@�Z���ł��B���̃��f���̑z��́A
����_�`��r���_�ŁA�u�~�J���͂S���l������v�A�u�����S�͒l�������Ȃ������v�ł����B
����_�̍w������́A�~�J����100�~�A�����S��300�~�ł��B
�@������d���Ζ@�Z���ł́A��r���_�̑���́A
����_�̑���ɉ��i�����{�ɂȂ������̔{�����|����Ώo�܂��B
�~�J���́A����_�̑����100�~��0.6�{����60�~����r���_�̑���B
�����S�́A����_�̑��300�~�̂P�{��300�~����r���_�̑���ƂȂ�܂��B
�@�~�J���ƃ����S�̍��v����́A����_400�~����r���_360�~�ł��B
����_��100�Ƃ�����r���_�̕����w����90�ł��B
��r���_��360�~������_��400�~�Ŋ����0.9�{�Ƃ����������o�Ă��܂��B
����0.9�{��100�{����90����r���_�̕����w���Ƃ����킯�ł��B
�@�����āA�E�G�C�g�Ɖ��i�w�����g�����v�Z�ł��B���̌v�Z�\�����Ă��������B
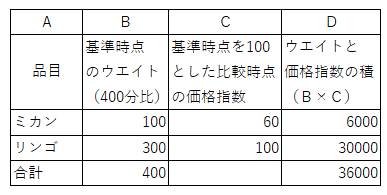
�@�a��̐������u�E�G�C�g�v�Ƃ��܂����B�����w���̐��E�ł̗p��ł��B
�������Ɋւ����ʓI�ȕ\�����Ɓu����v�B�����悤�Ȃ��̂ƍl���Ă��������B
�@���ڂ��Ă������������̂͂b��̐����ł��B
���i������_�����r���_�ɂ����ĉ��{�ɂȂ������́u�{���v�ł͂���܂���B
�{����100�{�����u���i�w���v�ɂȂ��Ă��܂��B
�@�c��́u�E�G�C�g�~���i�w���̐ρv���A���O�̌v�Z�\�̂c��̐�����100�{���������ɂȂ��Ă��܂��B
����̌v�Z�\�́A���O�̌v�Z�\�Ɣ�ׂ�ƁA�b���c��̐�����100�{�ɂȂ��Ă���킯�ł��B
�@���O�̌v�Z�\�ł͕����w�����v�Z����ہA���100�{���܂����B
��r���_�̍��v���������_�̍��v����Ŋ����āA���̌��100�{�����菇�ł��B
�@����̌v�Z�\�ł́A�O��100�{���Ă��܂��B
�e�i�ڂ̉��i�ω��̔{�������i�w���̐����ɂ���Ƃ���100���|���Ă���̂ł��B
�@���̂��߁A����̌v�Z�\�ł́A�c��̐����̍��v���a��̐����̍��v�Ŋ����������œ������o�܂��B
�u36000��400��90�v�������B����_��100�Ƃ�����r���_�̕����w���ł��B
�@�u�~100�v�̌v�Z��O�ɂ��Ă���ɂ��Ă����������͊ȒP�ł��B
�u�i�`�{�a�j�~100���i�`�~100�j�{�i�a�~100�j�v�Ƃ��������v���o���Ă��������B
�@�~�J���̉��i������_�`��r���_�ʼn��{�ɂȂ��������u�~�J�����i�̔{���v�ƕ\�L���܂��B
�����S�ł����l�̕\�L�����܂��B���̂Q�̌v�Z�������Ă��������B

��̎���������d���Ζ@�Z���ł��B
���̎��́u�~100�v�̏ꏊ���~�J�����i�̔{������S���i�̔{���̑O�Ɉڂ������ł��B
��̎��Ɖ��̎������������ł��邱�Ƃ́A�Q�̎��߂Ă���Ε�����܂��B
�@���̎��́u100�~�~�J�����i�̔{���v�̓~�J���̉��i�w���ł���A
�u100�~�����S���i�̔{���v�̓����S�̉��i�w���ł��B
�@����_�̃E�G�C�g�ɉ��i�w�����|����v�Z�́u������d���Ζ@�Z���Ǝ��������v�Ɣ[���ł���͂��ł��B
�e�i�ڂ̊�^�x���v�Z���邽�߂̍H�v
�@�����w���̕ω����ɑ���e�i�ڂ̉e���x�������l���邱�Ƃ͔��ɏd�v�ł��B
�s�����������ƂɁA�e�i�ڂ̉e���x�����́u��^�x�v�Ƃ��Ă�������v�Z�ł��܂��B
�@���i�w���̉��d���ς̌v�Z�\����|����Ɋ�^�x���v�Z���Ă݂܂��傤�B
�����ŏЉ��菇�́A�M�҂��Ǝ��ɍl���������̂ł��B
�܂��A���̌v�Z�\�����Ă��������B��قǂ܂ł́u�~�J���E�����S�����w�����f���v�ł��B
����́A�~�J������S�̃E�G�C�g���P������ɂ��Ă���܂��B
�����ȓ��v�ǂ́A�b�o�h���v�̑Ώۂ̑S�i�ڂ̍��v�E�G�C�g���P���ɂȂ�悤�ɐݒ肵�Ă��܂��B
����͂���ɏK���ĂP������ɂ��܂����B����x�o�̕i�ڂ��~�J���ƃ����S�����������f���ł��B
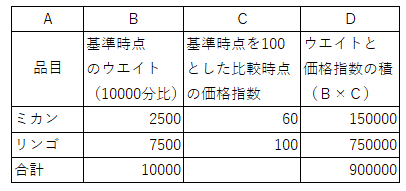
�@����_��100�Ƃ����r���_�̕����w���̌v�Z�̓X���[�Y�B
�e�i�ڂ́u�E�G�C�g�~���i�w���v�̐ς̍��v���e�i�ڂ̃E�G�C�g�̍��v�Ŋ��邾���ł��B
���̏ꍇ�ł́A�c��̍��v���a��̍��v�Ŋ���B�u90�����P����90�v�ƂȂ�܂��B
�@�����A���̌v�Z�\�����Ă��邾���ł́A�e�i�ڂ̊�^�x���ǂ��v�Z���邩�̃C���[�W�͗N���܂���B
�����ŁA�M�҂��l�������̂����̕\�ł��B
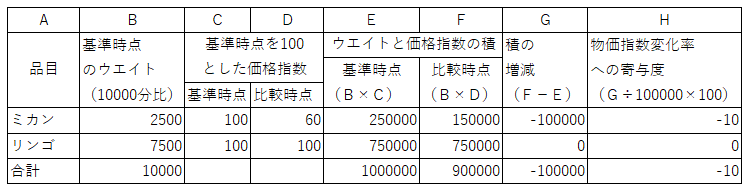
�@�b��A�d��A�f��A�g���V�݁B����_�Ɣ�r���_�̔������������ׂ�`�ɂ���̂��ړI�ł��B
���̂��߂̍H�v���b��ł��B����_��100�Ƃ��鉿�i�w��������_��100�Ȃ͓̂�����O�ł��B
����ł��A���̂b������邱�Ƃɂ���āA�������������ׂ�`�ɂȂ�܂��B
�@����_�Ɣ�r���_�ɂ��āA�~�J���̑���A�����S�̑���A���v������ׂ�킯�ł��B
�u�E�G�C�g�~���i�w���v�̐ς��������d��Ƃe������Ă��������B
�u�~�J���̑����10���~�������B�����S�̑���͕ς��Ȃ��B������A���v�����10���~���������v
���������\�}�������яオ���Ă��܂��B
�@�f��ɂ́A�e�i�ڂ̑���̑����z����ׂ܂��B
���̐���������_�̍��v����Ŋ�����100���|�����������e�i�ڂ̊�^�x�i�P�ʂ̓|�C���g�j�ł��B
������g��ɕ��ׂ܂��B�g��̐����̍��v�������w���ω����i�P�ʂ́��j�ł��B
�ʕi�ڂ̉e����������₷���u100���~�x�[�X�����������v
�@��قǐ��������P�[�X�́A�����w���̐����ɂ͎g�����肪�������̂��Ǝv���܂��B
�������������v�����100���~�ɂȂ�悤�ɐݒ肷��ƁA�����w���̎d�g�݂��������₷���̂ł��B
�����������̊G�ɂ��Ă݂��̂����̐}�ł��B�������茩�Ă��������B
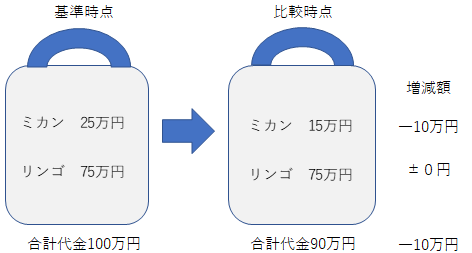
�@���v����́A����_��100���~�Ŕ�r���_��90���~�ł��B
�P���Ŋ����������������w���ɂȂ��Ă��܂��B����_100����r���_90�ł��B
�@����_�̑���́A�~�J����25���~�Ń����S��75���~�ł��B
�P���Ŋ��������������\���ł̎x�o�z�����ɂȂ��Ă��܂��B�~�J��25���A�����S75���ł��B
�@����̑����z�́A�~�J�����}�C�i�X10���~�B�����S�̓v���X�}�C�i�X�O�~�ł��B
�P���Ŋ�������������^�x�i�P�ʂ̓|�C���g�j�ł��B�~�J���̊�^�x�̓}�C�i�X10�|�C���g�ł��B
����_�̃E�G�C�g��������Őݒ肵�Ă���^�x�̌v�Z�l�͓���
�@�����w���̌v�Z�Ŏg���e�i�ڂ̃E�G�C�g�i�x�o�z�����j�ŏd�v�Ȃ̂́A�e�i�ڂ̔�ł��B
����܂Ő������Ă����u�~�J���E�����S�����w�����f���v�Ō����A
�u�~�J���P�F�����S�R�v�̔�ł��B
���̔���ێ����Ă���̂ł���A�E�G�C�g�͉�����ɂ��Ă����܂��܂���B
�@��Q�͂̐����ł́A�E�G�C�g��400����ɂ��Ă��܂����B���̌v�Z�\�̒ʂ�ł��B
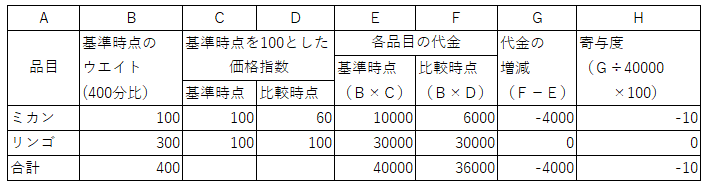
�@���̓E�G�C�g���P����ɂ����v�Z�\�����Ă�������
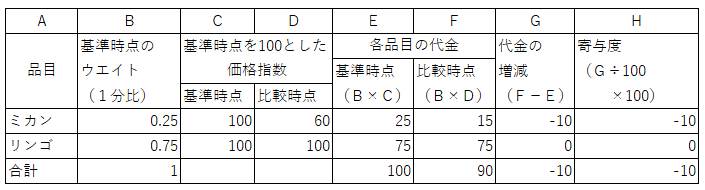
�@���̏ꍇ�A�������������v����́A����_��100�~�A��r���_��90�~�ƂȂ�܂��B
����͕����w���̐��ڂƂ܂��������������ł��B
�@�����āA�E�G�C�g���P������ɂ����v�Z�\���������������B
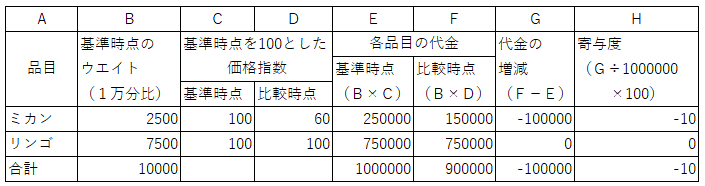
�@�E�G�C�g���P������ɂ���ƁA�u100���~�x�[�X�����������v�ɂȂ�܂��B
�@�E�G�C�g��������ɂ��Ă������̂͂Ȃ��ł��傤�B
������x�A�E�G�C�g���P����̌v�Z�\�����Ă��������B
�����āA�E�G�C�g��400����̌v�Z�\�ƌ���ׂĂ��������B
�@400����̌v�Z�\�͂P����̌v�Z�\�ɔ�ׁA
�a��A�d��A�e��A�f��̐�����400�{�ɂȂ��Ă��܂��B
400����̔������������v���������_�`��r���_�ʼn��{�ɂȂ������́A
�u36000�~�^40000�~�v�Ƃ����v�Z��0.9�{�ƂȂ�܂��B
���̌v�Z�́u90�~400�^100�~400�v�Ƃ����v�Z�Ɠ����ł��B
�u�~400�v�̕����́A����ƕ��q�̗��������菜���܂��B
��菜������̌v�Z�́u90�^100�v�ƂȂ�A�P����̌v�Z�Ƃ܂����������ɂȂ�܂��B
�@����ɍl���Ă݂܂��B�E�G�C�g���u�x����v�������Ƃ��܂��傤�B
�������������v��������{�ɂȂ������́u90�~�x�^100�~�x�v�Ƃ����v�Z�ɂȂ�܂��B
�u�~�x�v�̕����́A����ƕ��q�̗��������菜���܂��B
��菜������̌v�Z�́u90�^100�v�B�x�̓v���X�ł���A�ǂ�Ȑ����ł��n�j�ł��B
�@���̐}�����Ă��������B��r���_�̔������������v�����100���~�ɂ������̂ł��B
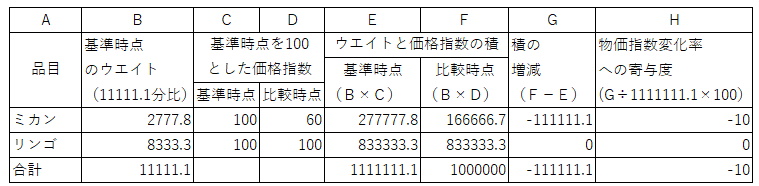
�@����_�̔������������v�����100���~�ɂ���Ƃ��́A
����_�̊e�i�ڂ̃E�G�C�g���P������ɂ��܂����B
��������ƁA�������������v�����100���~��90���~�Ƃ������ڂł����B
����́H���~��100���~�Ƃ������ڂɂ�������킯�ł��B
100���~��90���~��1.11111�{�Ȃ̂ŁA����_�̊e�i�ڂ̃E�G�C�g���P������łȂ��A
����1.11111�{��11111.1����ɂ�������킯�ł��B
��r���_�̍��v�����100���~�ɂ��Ă��e�i�ڂ̊�^�x�͕ς��܂���B
�v�Z�\���������茩�āA�m���߂Ă��������B
�g�b�v�y�[�W�ɖ߂�
















