僩僢僾儁乕僕偵栠傞
戞俀復丂暔壙巜悢偼攦偄暔偐偛僗僞僀儖偱寁嶼
丂偍偍偐偨偺恖偼乽擄偟偄栤戣乿偲姶偠傞偲丄怱偺拞偱偦偺栤戣傪墦偞偗傑偡丅
偦偟偰丄暔壙婾憰偼乽擄偟偄栤戣乿偲懡偔偺恖偑岆夝偟偰偄傑偡丅
丂暔壙巜悢偺寁嶼偺巇慻傒偼丄幚偼堄奜偵娙扨丅
偦偙傪愨懳偵暘偐偭偰傕傜偄偨偄丅偩偐傜丄愢柧偺巇曽偵岺晇傪廳偹偹偽乧丅
丂偙偺戞俀復偼丄昅幰偺嬯怱嶴滈偺枛偺嶻暔偱偡丅
乽嶼悢偺悽奅乿偺傗偝偟偄寁嶼峔憿
丂擄偟偦偆偵巚偊傞偺偼乽暔壙巜悢乿偲偄偆尵梩傕堦場偱偟傚偆丅
擄偟偄悢妛偺悽奅偵擖偭偰偄偔偲姶偠傞恖偑懡偄傛偆偱偡丅
幚嵺偵偼暔壙巜悢偺寁嶼偼丄懌偟嶼丄妡偗嶼丄堷偒嶼丄妱傝嶼偩偗偱偡傒傑偡丅
乽擔忢偺攦偄暔偺僀儊乕僕乿偱峫偊傞
丂暔壙巜悢偺寁嶼偺巇慻傒偑傗偝偟偄偺偼丄攦偄暔偐偛僗僞僀儖偵側偭偰偄傞偐傜偱偡丅
晛抜偺攦偄暔偺応柺傪巚偄晜偐傋側偑傜丄暔壙巜悢偺偙偲傪峫偊傑偟傚偆丅
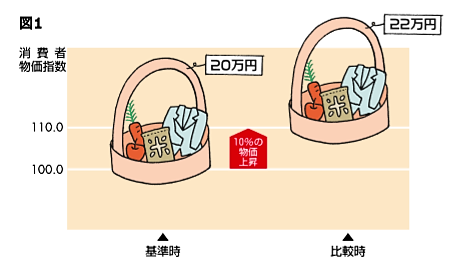
丂忋偺僀儔僗僩傪尒偰偔偩偝偄丅偄偄姶偠偺恾暱側偺偱丄庁梡偝偣偰偄偨偩偒傑偟偨丅
榓壧嶳導導柉惗妶壽敪峴偺儕乕僼儗僢僩乽傢偐傗傑暔壙偲偔傜偟乿偺2000擭俁寧崋偵嵹偭偰偄傑偟偨丅
攦偄暔偐偛偵偼丄暷丄僯儞僕儞丄儚僀僔儍僣偑擖偭偰偄傑偡丅
僀儔僗僩偑帵偟偰偄傞偺偼乽徚旓幰暔壙巜悢偺10亾忋徃乿偱偡丅
徚旓幰暔壙巜悢偺曄壔棪亖攦偄暔偐偛崌寁戙嬥偺曄壔棪
丂偙偺尒弌偟偺摍幃傪傑偢妎偊偰偔偩偝偄丅挻廳梫偱偡丅
擔忢偺惗妶姶妎偵傄偭偨傝増偆傕偺偩偲巚偄傑偡丅
暔壙偑忋偑傟偽丄攦偄暔偺偲偒偵昁梫側偍嬥偑憹偊傑偡丅
攦偄暔偐偛傪巊偆恖側傜丄偐偛偺拞偺偝傑偞傑側昳栚偺崌寁戙嬥偑憹偊傞傢偗偱偡丅
丂偙偺僀儔僗僩偱偼丄崌寁戙嬥偼20枩墌偐傜22枩墌偵10亾憹偊傑偟偨丅
攦偄暔偐偛崌寁戙嬥偺曄壔棪偼丄徚旓幰暔壙巜悢偺曄壔棪偲摨偠丅
偦偺偨傔丄偙偺応崌偼徚旓幰暔壙巜悢偺忋徃棪偑10亾偲側傝傑偡丅
丂乽徚旓幰暔壙巜悢傪偳偆寁嶼偡傞偐乿丅
偦傟偼乽攦偄暔偐偛偺崌寁戙嬥傪偳偆寁嶼偡傞偐乿偲偄偆偙偲偱偡丅
師偺寁嶼幃傕堄幆偟偰偔偩偝偄丅傑偭偨偔摉偨傝慜偺幃偱偡偑丄廳梫偱偡丅

丂攦偄暔偐偛偺崌寁戙嬥偼丄偐偛偺拞偺奺昳栚偺戙嬥偺崌寁丅
寢嬊丄奺昳栚偺戙嬥傪偳偆寁嶼偡傞偐傪偟偭偐傝峫偊側偄偲偄偗側偄偺偱偡丅
乽婎弨帪揰乿乽斾妑帪揰乿偲偼
丂暔壙巜悢偺寁嶼偺巇慻傒傪棟夝偡傞偨傔偵偼丄婎杮揑側偄偔偮偐偺梡岅偼妎偊偹偽側傝傑偣傫丅
愭傎偳偺僀儔僗僩偵弌偰偒偨乽婎弨帪乿乽斾妑帪乿偼丄旕忢偵昿斏偵弌偰偔傞梡岅偱偡丅
乽婎弨帪乿偼乽婎弨帪揰乿丄乽斾妑帪乿偼乽斾妑帪揰乿偲摨偠偱偡丅
丂斾妑帪揰偼丄暔壙巜悢傪嶼弌偟傛偆偲偟偰偄傞帪揰偱偡丅
偦偺斾妑帪揰偺暔壙巜悢偺悈弨傪帵偡偵偼丄婎弨偺帪揰偺暔壙巜悢偲斾傋傞偙偲偑昁梫丅
偦偺婎弨偺帪揰偑乽婎弨帪揰乿偱偡丅廬偭偰丄昁偢丄婎弨帪揰偼斾妑帪揰傛傝屆偄帪揰偵側傝傑偡丅
丂婎弨帪揰丄斾妑帪揰偲傕丄棟孅偺忋偱偼擭扨埵偵傕寧扨埵偵傕偱偒傑偡丅
幚柋忋偼丄婎弨帪揰偼擭扨埵偵偝傟傞偺偑晛捠偱偡丅
徚旓幰暔壙巜悢偺応崌偼丄枅寧丄岞昞帪揰偺慜寧偺悈弨偑岞昞偝傟傑偡丅
岞昞帪揰偺慜寧偑斾妑帪揰偵側偭偰偄傞傢偗偱偡丅
暔壙巜悢偼乽偳傫側悢抣丠乿乽偳偆寁嶼丠乿
丂懡偔偺昳栚偺壙奿偺摦偒傪暯嬒偟偨傕偺偑暔壙丅
偦偺暔壙偺摦偒傪昗弨抣偑100偺悢抣偱帵偟偨傕偺偑暔壙巜悢偱偡丅
婎弨帪揰傪100偲偡傞偺偑堦斒揑偱偡丅偦偺応崌偼丄
婎弨帪乣斾妑帪偱暔壙偑10亾忋偑偭偨偺側傜丄暔壙巜悢偼婎弨帪揰偑100偱,
斾妑帪揰偑110偲偄偆偙偲偵側傝傑偡丅乽暔壙偺10亾忋徃乿傪僀儊乕僕偟傗偡偄悢帤偱偡丅
丂婎弨帪揰傗斾妑帪揰偺攦偄暔偐偛崌寁戙嬥偑暘偐偭偰偄傟偽丄寁嶼偱偒傑偡丅
億僀儞僩偼乽婎弨帪揰乣斾妑帪揰偱崌寁戙嬥偑壗攞偵側偭偨偐乿偱偡丅
偦偺攞棪傪100攞偟偨悢抣偑斾妑帪揰偺暔壙巜悢偱偡丅
崌寁戙嬥偑壗攞偵側偭偨偐偼丄斾妑帪揰偺崌寁戙嬥傪婎弨帪揰偺崌寁戙嬥偱妱傟偽弌傑偡丅
偦傟傪100攞偡傞偺偩偐傜丄斾妑帪揰偺暔壙巜悢偺寁嶼幃偼師偺捠傝偵側傝傑偡丅

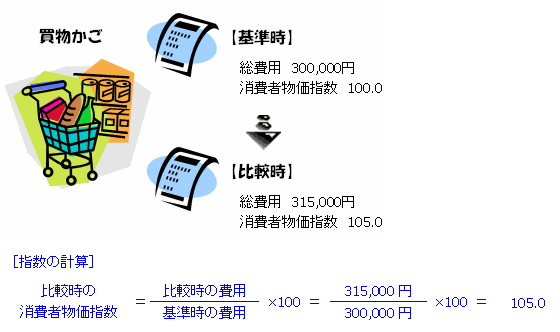
丂堬忛導摑寁壽嶌惉偺儂乕儉儁乕僕乽傆傞偝偲偍傕偟傠摑寁妛乿偵2008擭12寧偵宖嵹偝傟偨偺偑師偺僀儔僗僩丅
傗偼傝丄攦偄暔偐偛傪搊応偝偣偰偄傑偡丅
攦偄暔偐偛偺崌寁戙嬥傪乽憤旓梡乿偲偐乽旓梡乿偲屇傫偱偄傑偡偑丄撪梕偼摨庯巪丅
斾妑帪揰偺31枩5000墌傪婎弨帪揰偺30枩墌偱妱偭偰100傪妡偗偰偄傑偡丅
弌偰偒偨摎偊偼105丏暔壙巜悢偼丄婎弨帪揰偑100偱斾妑帪揰偑105偲偄偆偙偲偱偡丅
偙偺寁嶼庤弴偼丄愭傎偳昅幰偑帵偟偨寁嶼幃偦偺傑傑偱偡丅
壙奿巜悢偼乽偳傫側悢抣丠乿乽偳偆寁嶼丠乿
丂屄暿偺昳栚偺壙奿偺摦偒傪昗弨抣偑100偺悢抣偱昞偟偨偺偑壙奿巜悢偱偡丅
婎弨帪揰傪100偲偡傞壙奿巜悢偑堦斒揑偱偡丅
乽婎弨帪揰乣斾妑帪揰偱壙奿偑壗攞偵側偭偨偐乿偑傗偼傝億僀儞僩偱偡丅
偦偺攞棪傪100攞偟偨悢抣偑斾妑帪揰偺壙奿巜悢偱偡丅
偙偺応崌偺壙奿偼乽壗屄偱偄偔傜乿偺壙奿偱偼側偔丄乽侾屄偄偔傜乿偺乽扨壙乿偱偡丅
丂偁傞昳栚偺扨壙偑丄婎弨帪揰偵偼50墌丄斾妑帪揰偼40墌偩偭偨偲偟傑偡丅俀妱抣壓偑傝偱偡丅
偙偺昳栚偺乽婎弨帪揰傪100偲偡傞斾妑帪揰偺壙奿巜悢乿偼丄
40墌傪50墌偱妱偭偰100傪妡偗傟偽弌傑偡丅摎偊偼80偱偡丅
丂壙奿巜悢偼丄婎弨帪揰偑100丄斾妑帪揰偑80偱偡丅俀妱抣壓偑傝偑暘偐傝傗偡偄宍偱帵偣偰偄傑偡丅
婎弨帪揰傪100偲偡傞斾妑帪揰偺壙奿巜悢偼師偺寁嶼幃偱媮傔傑偡丅暔壙巜悢偦偭偔傝偱偡丅

椺奜揑偵斾妑帪揰偺巜悢傪100偲偡傞偙偲傕偁傞
丂暔壙巜悢傗壙奿巜悢偼乽斾乿偩偲峫偊傞偲棟夝偟傗偡偄偺偐傕偟傟傑偣傫丅
暔壙巜悢寁嶼梡偺攦偄暔偐偛偺崌寁戙嬥傪婎弨帪揰50枩墌丄斾妑帪揰40枩墌偲偟傑偡丅
婎弨帪揰乣斾妑帪揰偱崌寁戙嬥偼0.8攞偵側傝傑偟偨丅
偦傟傪100攞偟傑偡丅婎弨帪揰傪100偲偡傞斾妑帪揰偺暔壙巜悢偼80偱偡丅
乽50枩丗40枩乿亖乽1丗0.8乿亖乽100丗80乿偱偁傞偙偲傪妋偐傔偰偔偩偝偄丅
丂暔壙巜悢傗壙奿巜悢偼丄婎弨帪揰傪100偲偡傞偺偑晛捠偱偡偑丄椺奜揑偵斾妑帪揰傪100偲偡傞偙偲傕偁傝傑偡丅
攦偄暔偐偛崌寁戙嬥偑婎弨帪揰50枩墌丄斾妑帪揰40枩墌偱偁傞偲偒丄
斾妑帪揰偺暔壙巜悢傪100偲偡傞偵偼偳偆偡傟偽偄偄偺偱偟傚偆丅
偲傝偁偊偢丄婎弨帪揰偺崌寁戙嬥偑斾妑帪揰偺崌寁戙嬥偺壗攞偩偭偨偐傪峫偊傑偡丅
50枩墌傪40枩墌偱妱偭偰丄1.25攞偲暘偐傝傑偡丅偦傟傪100攞偟偰丄
斾妑帪揰偺暔壙巜悢傪100偲偡傞婎弨帪揰偺暔壙巜悢偺125傪偼偠偒弌偟傑偡丅
乽50枩丗40枩乿亖乽1丗0.8乿亖乽100丗80乿亖乽1.25丗1乿亖乽125丗100乿偲偄偆娭學傪妋偐傔偰偔偩偝偄丅
丂壙奿巜悢偺応崌傕摨條偵寁嶼偡傟偽偄偄偱偡丅
斾妑帪揰傪100偲偡傞婎弨帪揰偺暔壙巜悢傗壙奿巜悢偺寁嶼幃偼丄師偺捠傝偱偡丅

乽昳栚偲峸擖悢検偺屌掕乿偑寁嶼偺戝尨懃
丂偍懸偨偣偟傑偟偨丅偄傛偄傛丄攦偄暔偐偛偺崌寁戙嬥傪偳偆寁嶼偡傞偐峫偊傑偡丅
傑偢丄暔壙巜悢偺寁嶼偱偼婎弨帪揰偲斾妑帪揰偺昳栚傪姰慡偵堦抳偝偣傞偙偲偑戝尨懃偱偡丅
婎弨帪揰偵250昳栚偑擖偭偰偄偨攦偄暔偐偛偺偙偲傪峫偊傑偡丅
斾妑帪揰偵偼丄偦偺250昳栚偵5昳栚偑捛壛偝傟丄5昳栚偺戙嬥崌寁偑2枩墌偲偟傑偟傚偆丅
捛壛偝傟偨5昳栚埲奜偺250昳栚偺崌寁戙嬥偑婎弨帪揰偲斾妑帪揰偱摨偠100枩墌偩偭偨偲偟偰傕丄
斾妑帪揰偺攦偄暔偐偛崌寁戙嬥偼丄捛壛偝傟偨5昳栚偺戙嬥偺2枩墌偩偗懡偔側偭偰偟傑偄傑偡丅
丂偦偆偄偭偨偙偲偑婲偒側偄傛偆偵丄婎弨帪揰乣斾妑帪揰偺昳栚傪傄偭偨傝偦傠偊傞偺偱偡丅
昳栚傪偦傠偊傞偙偲偑斾妑偺慜採偲側傞偺偼丄忢幆偺斖埻撪偵傕巚偊傑偡丅

丂傕偆侾偮偺戝尨懃偼乽婎弨帪揰乣斾妑帪揰偱奺昳栚偺峸擖悢検偑曄傢傜側偄乿偲壖掕偡傞偙偲偱偡丅
側偤丄偦傟偑昁梫偐丅儈僇儞偲儕儞僑偺俀昳栚偩偗偺乽儈僇儞丒儕儞僑暔壙巜悢儌僨儖乿偱峫偊傑偡丅
偙偺戞俀復偱偼丄偙偺儌僨儖偱偢偭偲峫偊偰偄偒傑偡丅儌僨儖偺憐掕忦審偼師偺捠傝偱偡丅
亂婎弨帪揰偵偼丄1屄50墌偺儈僇儞傪2屄丄1屄100墌偺儕儞僑傪3屄攦偭偨丅
斾妑帪揰偱偼丄儈僇儞偼1屄30墌偵抣壓偑傝偟偰偄偨偺偱婐偟偔側偭偰4屄攦偄丄
儕儞僑偼抣抜偑曄傢傜側偐偭偨偺偱丄婎弨帪揰偲摨偠偔3屄攦偭偨亃
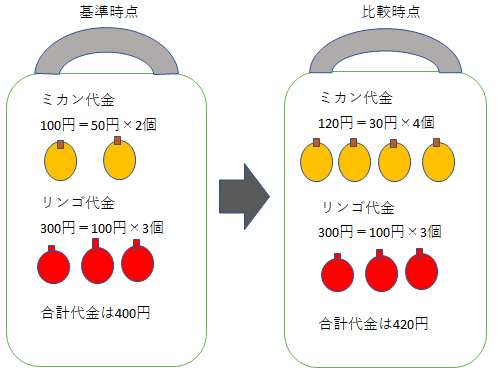
丂儕儞僑偺壙奿偼曄傢傜偢丄儈僇儞偼抣壓偑傝偟偨偺偱丄暔壙悈弨偼壓偑偭偨偼偢偱偡丅
偟偐偟丄憐掕忦審捠傝偵寁嶼偡傞偲丄偦偆偄偭偨寁嶼寢壥偵偼側傝傑偣傫丅
攦偄暔偐偛偺崌寁戙嬥偼丄婎弨帪揰偼乽儈僇儞50墌亊2屄亖100墌乿乽儕儞僑100墌亊3屄亖300墌乿偺崌寁400墌丅
斾妑帪揰偼乽儈僇儞30墌亊4屄亖120墌乿乽儕儞僑100墌亊3屄乿偺崌寁偱420墌丅
攦偄暔偐偛崌寁戙嬥偼5亾偺憹壛偵側偭偰偟傑偄傑偟偨丅
丂暔壙巜悢偺寁嶼偱偼乽攦偄暔崌寁戙嬥偺曄壔棪亖暔壙巜悢偺曄壔棪乿偲側傞偼偢偱偡丅
側偤偦偆側傜側偄偺偱偟傚偆丅摎偊偼娙扨丅壙奿埲奜偺梫場偑寁嶼偵塭嬁偟偰偄傞偨傔偱偡丅
偙偺儌僨儖偱偼丄婎弨帪揰乣斾妑帪揰偱儈僇儞偺峸擖屄悢偑2攞偵憹偊偰偄傑偡丅
偦偺悢検憹壛偺梫場偲壙奿壓棊偺梫場偑偛偭偪傖偵側偭偰暘偐傝偵偔偔側偭偰偄傞偺偱偡丅
丂偦偆偄偭偨偙偲偵側傜側偄傛偆丄暔壙巜悢偺寁嶼偱偼壖掕偺忦審傪愝偗偰寁嶼偟傑偡丅
乽婎弨帪揰乣斾妑帪揰偱奺昳栚偺悢検偑曄傢傜側偄乿偲偄偆壖掕偱偡丅
丂偙偺壖掕偵傛偭偰丄奺昳栚偺戙嬥偼壙奿偺曄壔偵姰慡偵斾椺偟偰曄壔偡傞傛偆偵側傝傑偡丅
婎弨帪揰乣斾妑帪揰偱儈僇儞偺壙奿偑0.6攞偵側傟偽丄儈僇儞偺戙嬥傕0.6攞偵側傞偺偱偡丅
丂乽攦偄暔偐偛偺拞偺昳栚傗奺昳栚偺悢検傪屌掕偟偰寁嶼偡傞乿偲偄偆庤朄偼丄暔壙巜悢寁嶼偺堦斣偺梫丅
偙偺偁偨傝偺偙偲偼丄偟偭偐傝擖擮偵摢偵偨偨偒偙傫偱偍偔傋偒偱偡丅
憤柋徣摑寁嬊偺俠俹俬偺僒僀僩偵偼乽徚旓幰暔壙巜悢偺嶌傝曽乿偲偄偆僐乕僫乕偑偁傝傑偡丅
偦偺俉儁乕僕偵偼丄偙偺婎杮偑偟偭偐傝愢柧偟偰偁傝傑偡丅壓偺夋憸偱妋偐傔偰偔偩偝偄丅

丂偨偩丄悢検偵偮偄偰偼丄偳偺帪揰偺悢検偱屌掕偡傞偐偲偄偆栤戣偑偁傝傑偡丅
偙偺栤戣傊偺懳墳偱丄儔僗僷僀儗僗曽幃偲僷乕僔僃曽幃偺堘偄偑惗偠傑偟偨丅
婎弨帪揰偺悢検偱屌掕偡傞儔僗僷僀儗僗曽幃
丂暔壙巜悢寁嶼偺悽奅偱偼丄儔僗僷僀儗僗曽幃偲僷乕僔僃曽幃偑桳柤偱偡丅
儔僗僷僀儗僗巵傕僷乕僔僃巵傕19悽婭屻敿偵妶桇偟偨僪僀僣偺宱嵪傗摑寁偺妛幰偱偡丅
暔壙巜悢偺寁嶼曽幃傪傔偖偭偰媍榑偟偰偄偨偺偼丄擔杮偱尵偊偽丄柧帯堐怴偺崰偱偡丅
儔僗僷僀儗僗巜悢丄僷乕僔僃巜悢偲偄偆尵梩傕傛偔巊傢傟傑偡丅
2恖偲傕丄暔壙巜悢寁嶼梡攦偄暔偐偛偺拞偺奺昳栚偺戙嬥偼丄師偺幃偱寁嶼偟偰偄傑偟偨丅

丂晛捠偱偛偔摉偨傝慜偺寁嶼曽朄偱偡丅2恖偺堘偄偼丄奺昳栚偺悢検傪偳偺抧揰偺傕偺偱屌掕偡傞偐丅
儔僗僷僀儗僗巵偼丄婎弨帪揰偺悢検偱屌掕偡傞偙偲傪採彞偟傑偟偨丅
乽婎弨帪揰偺攦偄暔偺巇曽偑斾妑帪揰傑偱懕偔乿偲偄偭偨峫偊曽偱偡丅
丂愭傎偳偺儈僇儞丒儕儞僑暔壙巜悢儌僨儖偱峫偊偰傒傑偟傚偆丅儌僨儖偺憐掕忦審偼師偺捠傝偱偡丅

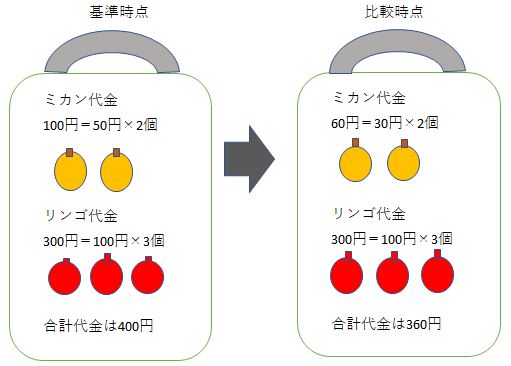
丂寁嶼寢壥偼師偺恾偺捠傝偱偡丅婎弨帪揰丄斾妑帪揰偲傕儈僇儞偺悢検偼婎弨帪揰偺2屄偲側傝傑偡丅
攦偄暔偐偛崌寁戙嬥偼丄婎弨帪揰偼乽儈僇儞50墌亊2屄亖100墌丄儕儞僑100墌亊3屄亖300墌乿偺崌寁偱400墌丅
斾妑帪揰偼乽儈僇儞30墌亊2屄亖60墌丄儕儞僑100墌亊3屄亖300墌乿偺崌寁偱360墌偱偡丅
婎弨帪揰傪100偲偡傞斾妑帪揰偺暔壙巜悢偼乽360墌亐400墌亊100乿偱90偲側傝傑偡丅
暔壙巜悢偼婎弨帪揰乣斾妑帪揰偱10亾壓棊偟偨傢偗偱偡丅
丂崱偺寁嶼庤弴傪堦斒揑側幃偵偡傞偲師偺捠傝偵側傝傑偡丅

丂俹偲偐俻偲偐儼乮僔僌儅乯偺傛偆側婰崋偱昞偡偙偲偑晛捠偱偡丅
偟偐偟丄偦偆偟偨婰崋偵傛偭偰乽擄偟偄栤戣乿偲巚偆恖偑懡偄偺偱丄晛捠偺擔杮岅偱昞婰偟傑偡丅
丂徚旓幰暔壙巜悢偺幚嵺偺寁嶼偱偼丄懳徾偺昳栚偑悢昐偁傝傑偡丅
寁嶼嶌嬈偼戝曄偵巚偊傑偡偑丄幚嵺傗偭偰傒傞偲堄奜側傎偳妝偱偡丅
師偺傛偆側宍偱丄帺暘偺僷僜僐儞偱僄僋僙儖傪巊偭偰僗儉乕僘偵寁嶼偱偒傞偐傜偱偡丅

斾妑帪揰偺悢検偱屌掕偡傞僷乕僔僃曽幃
儔僗僷僀儗僗曽幃偺峫偊曽偼乽婎弨帪揰偺攦偄暔偺巇曽傪斾妑帪揰偵傕偡傞偲攦偄暔偐偛偺崌寁戙嬥偼偳偆曄傢傞偐B
壙奿曄壔偵傛偭偰奺昳栚偺斾妑帪揰偺峸擖悢検偑曄傢傞尰幚傪柍帇偟偰偄傑偡丅
偦偙偱丄僷乕僔僃巵偼暿偺峫偊曽傪採彞偟傑偟偨丅
乽斾妑帪揰偺攦偄暔偺巇曽傪婎弨帪揰偵傕偟偰偄偨傜攦偄暔偐偛偺崌寁戙嬥偼偳偆曄傢傞偐乿丅
斾妑帪揰偱偺奺昳栚偺峸擖悢検偑婎弨帪揰偱傕摨偠偩偭偨偲偄偆壖掕偱寁嶼偡傞傢偗偱偡丅
丂崱夞傕儈僇儞丒儕儞僑暔壙巜悢儌僨儖偱峫偊傑偡丅儌僨儖偺憐掕忦審偼師偺捠傝偱偡丅

丂寁嶼寢壥偼師偺恾偺捠傝偱偡丅婎弨帪揰丄斾妑帪揰偲傕儈僇儞偺悢検偼斾妑帪揰偺4屄偲側傝傑偡丅
攦偄暔偐偛崌寁戙嬥偼丄婎弨帪揰偼乽儈僇儞50墌亊4屄亖200墌丄儕儞僑100墌亊3屄亖300墌乿偺崌寁偱500墌丅
斾妑帪揰偼乽儈僇儞30墌亊4屄亖120墌丄儕儞僑100墌亊3屄亖300墌乿偺崌寁偱420墌偱偡丅
婎弨帪揰傪100偲偡傞斾妑帪揰偺暔壙巜悢偼乽420墌亐500墌亊100乿偱84偲側傝傑偡丅
暔壙巜悢偼婎弨帪揰乣斾妑帪揰偱16亾壓棊偟偨傢偗偱偡丅
丂偙偺儌僨儖偱偼暔壙巜悢偺壓棊棪偼丄儔僗僷僀儗僗曽幃偱偼10亾丄僷乕僔僃曽幃偱偼16亾丅
僷乕僔僃曽幃偺曽偑壓棊棪偑戝偒偄偺偼丄婎弨帪揰乣斾妑帪揰偱儈僇儞偺峸擖悢検偑2攞偵憹偊偨偐傜偱偡丅
峸擖悢検偑2攞偵憹偊偨斾妑帪揰偺悢検偱屌掕偝偣偰寁嶼偡傞偺偱丄
僷乕僔僃曽幃偺偲偒偼儈僇儞偺抣壓偑傝偺塭嬁偑戝偒偔側傞偺偱偡丅
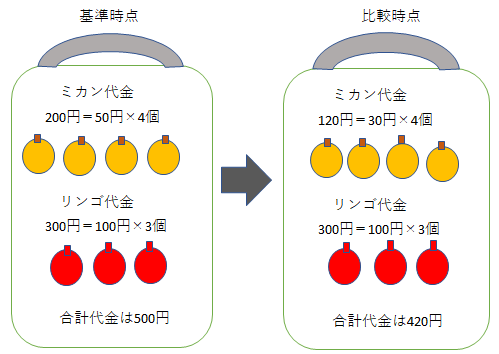
丂僷乕僔僃曽幃偺寁嶼曽朄傪堦斒揑偵彂偔偲丄師偺捠傝偱偡丅

丂僷乕僔僃曽幃傕師偺傛偆偵昞偺宍偱寁嶼偱偒傑偡丅
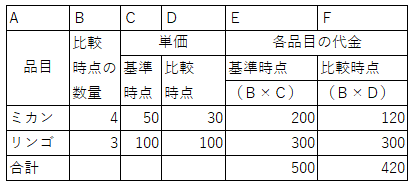
悢検傪巊傢側偄偱偡傑偡曄宍偺寁嶼幃
丂暔壙巜悢偺弶曕揑側夝愢偱偼丄奺昳栚偺戙嬥偼乽悢検亊壙奿乿偱寁嶼偡傞偲愢柧偟傑偡丅
偲偙傠偑丄徚旓幰暔壙巜悢傪寁嶼偡傞尰応偱偼丄悢検偺僨乕僞傪巊偄傑偣傫丅悢検偺愝掕偑偱偒側偄偺偱偡丅
憤柋徣摑寁嬊偼乽岎捠旓傗堛椕旓偵偮偄偰偼摑堦揑側扨埵偱悢検傪挷傋傞偙偲偑擄偟偄乿側偳偲愢柧偟傑偡丅
丂崲偭偨傛偆偱偡偑丄悢検傪巊傢側偄偱偡傑偡恑壔偟偨寁嶼曽朄偑偁傝傑偡丅
悢検傪屌掕偡傞帪揰偺奺昳栚偺戙嬥傪傕偲偵暿偺帪揰偺奺昳栚偺戙嬥傪媮傔傞曽朄偱偡丅
偙偺曽朄偼岻柇偱偼偁傞傕偺偺棟夝偟偵偔偄丅椺傪弌偟傑偡偺偱丄偠偭偔傝峫偊偰傒偰偔偩偝偄丅
丂偁傞昳栚偺俙帪揰偺戙嬥偼暘偐偭偰偄偰丄懠偺帪揰偺峸擖悢検傕丄俙帪揰偺悢検偱曄傢傜側偄偲壖掕偟傑偡丅
俙帪揰偲俛帪揰偺壙奿乮扨壙乯偑暘偐偭偰偄傟偽丄俛帪揰偺戙嬥偼師偺幃偱寁嶼偱偒傑偡丅
俛帪揰偑俙帪揰傛傝慜偐屻偐偼娭學偁傝傑偣傫丅

丂俙帪揰偺悢検偱屌掕偡傞偲偄偆栺懇偑偁傞側傜丄俛帪揰偺戙嬥偼丄俙帪揰偺戙嬥偵
乽俛帪揰偺壙奿偼俙帪揰偺壙奿偺壗攞偐乿偺曄壔攞棪乮壙奿斾乯傪妡偗傟偽弌偣傑偡丅
偙偺愢柧暥傪寁嶼幃偵偟偨偺偑丄偙偺恾偺幃偱偡丅
丂俛帪揰偺戙嬥傪乽壙奿乮扨壙乯亊悢検乿偱寁嶼偡傞偲偒偼丄懠偺帪揰偺帠忣偼娭學偁傝傑偣傫丅
崱愢柧偟偰偄傞寁嶼曽朄偼偦偆偱偼側偔丄俛帪揰偺戙嬥偑俙帪揰偺戙嬥偲偺憡懳揑側娭學偱寛傑傝傑偡丅
俙帪揰偲俛帪揰偺壙奿偺斾偑丄俙帪揰偲俛帪揰偺戙嬥偺斾偲摨偠偵側傞偙偲傪棙梡偟偨寁嶼曽朄偱偡丅
丂擔忢揑側攦偄暔偱峫偊傑偟傚偆丅俙帪揰偵1杮30墌偺僶僫僫傪10杮攦偭偨偲壖掕偟傑偡丅
俛抧揰偵偼僶僫僫偼1杮39墌偩偭偨偲偟傑偡丅壙奿偼1.3攞偱偡丅
俙帪揰偺悢検偱屌掕偡傞偺偱丄寁嶼忋偼俛帪揰偺僶僫僫偺杮悢傕10杮偵側傝傑偡丅
僶僫僫偺戙嬥偼丄俙帪揰偼乽30墌亊10杮亖300墌乿丄俛抧揰偼乽39墌亊10杮亖390墌乿偱偡丅
丂俙帪揰偺僶僫僫戙嬥偑300墌丄壙奿曄壔偺攞棪乮俛帪揰偺壙奿亐俙帪揰偺壙奿乯偑1.3攞偲暘偐偭偰偄傞偲丄
乽杮悢偼壗杮丠乿側偳偲峫偊偢偵丄暿儖乕僩偱寁嶼偱偒傑偡丅
俙帪揰偺僶僫僫戙嬥偺300墌傪1.3攞偟偰俛帪揰偺僶僫僫戙嬥傪390墌偲偼偠偒弌偣傞偺偱偡丅
僶僫僫偺壙奿偼俛帪揰偑俙帪揰偺1.3攞丅偩偐傜丄僶僫僫偺戙嬥傕俛帪揰偑俙帪揰偺1.3攞偵側傞棟孅偱偡丅
僶僫僫偺壙奿乮扨壙乯偲戙嬥偺娭學傪昞偵傑偲傔偨偺偱丄妋擣偟偰偔偩偝偄丅
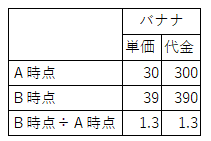
丂乽偙傫側姶偠偺寁嶼側傜丄擔乆偺攦偄暔偺偲偒偵偄偮傕傗偭偰偄傞乿偲偆側偢偔恖傕偄傞偼偢偱偡丅
幚梡惈偑崅偄恑壔宯偺儔僗僷僀儗僗曽幃
丂愭傎偳偺寁嶼幃傪傕偆堦搙傛偔尒偰偔偩偝偄丅
俙帪揰偑婎弨帪揰丄俛帪揰偑斾妑帪揰側傜丄師偺恾偺幃偵側傝傑偡丅

丂斾妑帪揰偺奺昳栚偺戙嬥偑崱偺幃偱弌偣傞偺偱丄崌寁戙嬥傕偮偐傔傑偡丅
斾妑帪揰偺崌寁戙嬥傪婎弨帪揰偺崌寁戙嬥偱妱偭偰100傪妡偗傟偽丄
婎弨帪揰傪100偲偟偨斾妑帪揰偺暔壙巜悢偑嶼弌偱偒傑偡丅幃偵偡傞偲丄師偺捠傝丅

丂偙傟偑乽婎弨帪壛廳憡懳朄嶼幃乿偲屇偽傟傞寁嶼曽幃偱偡丅
儔僗僷僀儗僗曽幃傪曄宍偝偣偨幃偱偁傝丄撪梕揑偵偼儔僗僷僀儗僗曽幃偲摨偠偱偡丅
丂嵞傃丄椺偺儈僇儞丒儕儞僑暔壙巜悢儌僨儖偱峫偊傑偡丅儌僨儖偺愝掕忦審偼師偺捠傝偱偡丅

丂婎弨帪壛廳憡懳朄嶼幃傪摉偰偼傔偨寁嶼寢壥偼師偺恾偵側傝傑偡丅
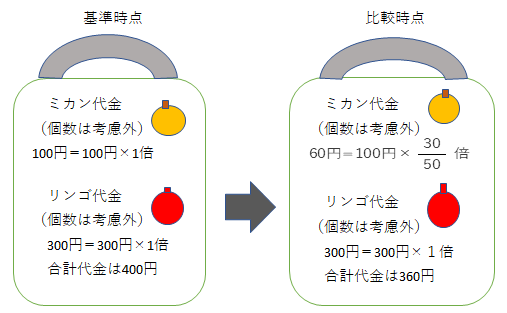
丂婎弨帪揰偺悢検偱屌掕偡傞偺偑儔僗僷僀儗僗曽幃丅偙偺曽幃偱悢検傪峫偊偢偵寁嶼偡傞偵偼丄
奺昳栚偺婎弨帪揰偺戙嬥偵乽斾妑帪揰偺壙奿偼婎弨帪揰偺壙奿偺壗攞偐乿偺攞棪傪妡偗傑偡丅
偙偺儌僨儖偱偼丄壙奿曄壔偺側偄儕儞僑偺戙嬥偼丄婎弨帪揰丄斾妑帪揰偲傕300墌偱偡丅
丂堦曽丄儈僇儞偺婎弨帪揰偺戙嬥偼100墌偱偡丅
儈僇儞偺斾妑帪揰偺戙嬥偼丄100墌偵壙奿曄壔偺攞棪傪妡偗偰弌偟傑偡丅
儈僇儞偺扨壙偼50墌仺30墌偲偄偆悇堏側偺偱丄壙奿曄壔偺攞棪偼乽30乛50攞乿偮傑傝0.6攞偱偡丅
寢嬊丄儈僇儞偺斾妑帪揰偺戙嬥偼乽100墌亊0.6乿偲偄偆寁嶼偱60墌偲側傝傑偡丅
丂攦偄暔偐偛崌寁戙嬥偼丄婎弨帪揰偼儈僇儞100墌丄儕儞僑300墌偺崌寁偱400墌丅
斾妑帪揰偼儈僇儞60墌丄儕儞僑300墌偺崌寁偱360墌偱偡丅
攦偄暔偐偛崌寁戙嬥偼400墌仺360墌偺悇堏側偺偱丄暔壙巜悢偼100仺90偲側傝傑偡丅
丂婎弨帪壛廳憡懳朄嶼幃傕丄昳栚偑悢昐偁偭偰傕師偺傛偆偵昞偺宍偱僗儉乕僘偵寁嶼偱偒傑偡丅
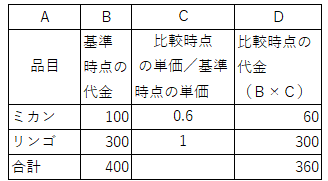
丂婎弨帪壛廳憡懳朄嶼幃偼丄幚梡惈偑嬌傔偰崅偄偺偑摿挿偱偡丅
奺昳栚偺壙奿曄壔棪偼丄挷嵏堳偑揦摢壙奿傪挷傋傞曽朄偱摑寁傪惍旛偱偒傑偡丅
丂婎弨帪揰偺奺昳栚偺戙嬥傕丄懡偔偺壠掚傊偺傾儞働乕僩挷嵏偱攃埇偟偨巟弌妟妱崌偐傜愝掕偱偒傑偡丅
婎弨帪揰偵侾夞丄戝婯柾偵傾儞働乕僩挷嵏傪偡傟偽丄
奺昳栚偺婎弨帪揰偺戙嬥偲壙奿曄壔棪偐傜暔壙巜悢偑寁嶼偱偒傞偺偱偡丅
偙偺偨傔丄悽奅偺懡偔偺崙偑婎弨帪壛廳憡懳朄嶼幃傪巊偭偰暔壙巜悢傪寁嶼偟偰偄傑偡丅
恑壔宯偱傕幚梡壔偱偒側偄僷乕僔僃曽幃
丂悢検傪巊傢側偄偱寁嶼偡傞儔僗僷僀儗僗曽幃偑乽婎弨帪壛廳憡懳朄嶼幃乿偱偟偨丅
偦傟偲暲傇偺偑丄悢検傪巊傢側偄偱寁嶼偡傞僷乕僔僃曽幃偱偁傞乽斾妑帪壛廳憡懳朄嶼幃乿偱偡丅
僷乕僔僃曽幃側偺偱丄斾妑帪揰偺悢検偱屌掕偡傞偺偑寛傑傝丅奺昳栚偺斾妑帪揰偺戙嬥偑暘偐偭偰偄傟偽丄
斾妑帪揰偺戙嬥偵乽婎弨帪揰偺扨壙偼斾妑帪揰偺扨壙偺壗攞偩偭偨偐乿偺攞棪傪妡偗傟偽俷俲丅
師偺寁嶼幃偱丄奺昳栚偺婎弨帪揰偺戙嬥偑偼偠偒弌偣傑偡丅

丂偙偺寁嶼幃傪傕偲偵奺昳栚偺婎弨帪揰偺崌寁戙嬥偑寁嶼偱偒傑偡丅
偦偟偰丄斾妑帪揰偺崌寁戙嬥傪婎弨帪揰偺崌寁戙嬥偱妱偭偰100傪妡偗傞偲丄
婎弨帪揰傪100偲偟偨斾妑帪揰偺暔壙巜悢偵側傝傑偡丅偦偺宍偵偟偨寁嶼幃偼師偺捠傝偱偡丅

丂偙傟偑乽斾妑帪壛廳憡懳朄嶼幃乿偱偡丅
僷乕僔僃曽幃傪曄宍偝偣偨幃偱偁傝丄撪梕揑偵偼僷乕僔僃曽幃偲摨偠偱偡丅
丂傑偨傑偨丄儈僇儞丒儕儞僑暔壙巜悢儌僨儖偱峫偊傑偡丅儌僨儖偺愝掕忦審偼師偺捠傝偱偡丅

丂斾妑帪壛廳憡懳朄嶼幃傪摉偰偼傔偨寁嶼寢壥偼師偺恾偵側傝傑偡丅
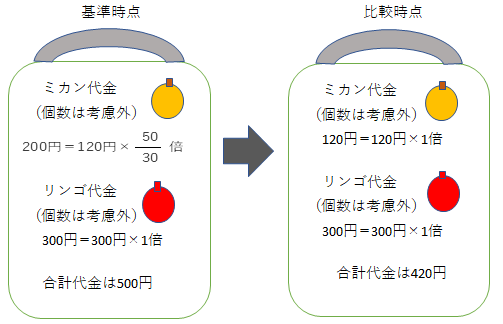
丂斾妑帪揰偺悢検偱屌掕偡傞偺偑僷乕僔僃曽幃偱偡丅偙偺曽幃偱悢検傪峫偊偢偵寁嶼偡傞偵偼丄
奺昳栚偺斾妑帪揰偺戙嬥偵乽婎弨帪揰偺壙奿偼斾妑帪揰偺壙奿偺壗攞偐乿偺攞棪傪妡偗傑偡丅
偙偺儌僨儖偱偼丄壙奿曄壔偺側偄儕儞僑偺戙嬥偼丄婎弨帪揰丄斾妑帪揰偲傕300墌偱偡丅
丂堦曽丄儈僇儞偺斾妑帪揰偺戙嬥偼120墌偱偡丅
儈僇儞偺婎弨帪揰偺戙嬥偼丄120墌偵壙奿曄壔偺攞棪傪妡偗偰弌偟傑偡丅
儈僇儞偺扨壙偼婎弨帪揰50墌仺斾妑帪揰30墌偲偄偆悇堏偱偡丅
婎弨帪揰偺扨壙偑斾妑帪揰偺壗攞偩偭偨偐偼乽50亐30乿偱1.666攞偱偡丅
寢嬊丄儈僇儞偺婎弨帪揰偺戙嬥偼乽120墌亊1.666乿偲偄偆寁嶼偱200墌偲側傝傑偡丅
丂攦偄暔偐偛崌寁戙嬥偼丄婎弨帪揰偼儈僇儞200墌丄儕儞僑300墌偺崌寁偱500墌丅
斾妑帪揰偼儈僇儞120墌丄儕儞僑300墌偺崌寁偱420墌偱偡丅
攦偄暔偐偛崌寁戙嬥偼500墌仺420墌偺悇堏側偺偱丄暔壙巜悢偼100仺84偲側傝傑偡丅
丂斾妑帪壛廳憡懳朄嶼幃傕丄師偺傛偆偵昞偺宍偱僗儉乕僘偵寁嶼偱偒傑偡丅
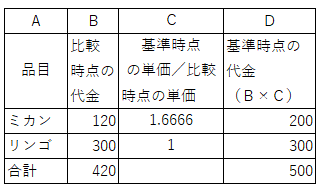
丂僷乕僔僃曽幃偺曄宍偱偁傞斾妑帪壛廳憡懳朄嶼幃傕丄幚梡惈偼偁傝傑偣傫丅
暔壙巜悢偺寁嶼偼丄扴摉婡娭偵傛偭偰枅寧峴傢傟傑偡丅斾妑帪揰偼嵟怴偺帪揰偱偡丅
斾妑帪揰偺奺昳栚偺戙嬥傪愝掕偡傞偵偼丄斾妑帪揰偵戝妡偐傝側傾儞働乕僩挷嵏傪偟偰丄
斾妑帪揰偺奺昳栚偺巟弌妟妱崌傪偮偐傓昁梫偑偁傝傑偡偑丄
枅寧戝妡偐傝側傾儞働乕僩挷嵏傪偟偰丄嵟怴帪揰偺巟弌妟妱崌傪偮偐傓偺偼崲擄偱偡丅
壛廳憡懳朄嶼幃偺惓偟偝傪幃偺曄宍偱妋擣
丂偙偙傑偱偺愢柧偱偼丄婎弨帪壛廳憡懳朄嶼幃傗斾妑帪壛廳憡懳朄嶼幃偑擄偟偄姶偠丅
偦偙偱丄椉曽幃偵偮偄偰偝傜偵愢柧偟傑偡丅
寁嶼幃偺曄宍傪偄傠偄傠傗偭偰傒傞偲丄椉曽幃偺堄枴偡傞偲偙傠偑傛偔暘偐偭偰偒傑偡丅
傑偢丄師偺嘆偺幃傪尒偰偔偩偝偄丅

丂偙傟偼丄屄暿昳栚偺戙嬥偑婎弨帪揰乣斾妑帪揰偱壗攞偵側偭偨偐傪偼偠偒弌偡寁嶼幃偱偡丅
暔壙巜悢偺寁嶼偱偼丄婎弨帪揰偲斾妑帪揰偺悢検偑摨偠偲壖掕偟傑偡丅
嘆偺幃偺塃曈偺暘曣偲暘巕偵偼摨偠悢検偑妡偐偭偰偄傞偙偲偵側傞偺偱丄
偦偺悢検偱暘曣偲暘巕偦傟偧傟傪妱傞偲丄師偺嘇偺幃偵側傝傑偡丅
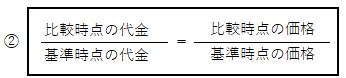
丂嘇偺幃傪傛偔尒偰偔偩偝偄丅婎弨帪揰偲斾妑帪揰偺戙嬥傗扨壙偵偮偄偰
乽戙嬥偑壗攞偵側偭偨偺偐偲丄扨壙偑壗攞偵側偭偨偺偐偺攞棪偼摨偠乿偲偄偆堄枴偱偡丅
偙偺偁偨傝偑暔壙寁嶼偺僉乕億僀儞僩偱偡丅
丂懕偄偰丄嘇偺幃偺椉曈偵乽婎弨帪揰偺戙嬥乿傪妡偗傑偡丅偡傞偲嘊偺幃偵側傝傑偡丅

丂偙傟偼丄婎弨帪壛廳憡懳朄嶼幃偱丄斾妑帪揰偺戙嬥傪媮傔傞寁嶼幃偱偡丅
丂愭傎偳偺嘇偺幃偼丄椉曈偺暘曣偲暘巕傪傂偭偔傝曉偡偙偲偑偱偒傑偡丅
偡傞偲丄師偺嘋偺幃偵側傝傑偡丅

丂偙偺嘋偺幃偺椉曈偵乽斾妑帪揰偺戙嬥乿傪妡偗傞偲丄嘍偺幃偵側傝傑偡丅

崱搙偼丄斾妑帪壛廳憡懳朄嶼幃偱丄婎弨帪揰偺戙嬥傪媮傔傞寁嶼幃偱偡丅
丂娙扨側寁嶼幃偺曄宍偵傛偭偰乽壛廳憡懳朄嶼幃乿偺惓偟偝偼棫徹偱偒傞偺偱偡丅
乽壛廳暯嬒乿乽僂僄僀僩乿傕棟夝偟偰偍偙偆
丂偙偺戞2復偱偼乽婎弨帪壛廳憡懳朄嶼幃乿乽斾妑帪壛廳憡懳朄嶼幃乿偲偄偆尵梩偑弌偰偄傑偡丅
乽壛廳偭偰壗乿偲姶偠偨恖傕偄傞偼偢側偺偱丄壛廳偲偼壗偐傪峫偊傑偡丅
儈僇儞丒儕儞僑暔壙巜悢儌僨儖偺婎弨帪壛廳憡懳朄嶼幃偺寁嶼昞傪嵞宖偟傑偡丅
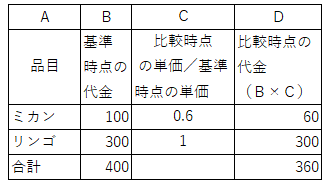
丂偙偺昞偺俠楍偺乽儈僇儞0.6乿乽儕儞僑1乿偺悢帤偼丄
儈僇儞傗儕儞僑偺扨壙偑婎弨帪揰乣斾妑帪揰偱壗攞偵側偭偨偐偺曄壔攞棪乮壙奿斾乯偱偡丅
丂偙偺曄壔攞棪偺暯嬒傪弌偟傑偟傚偆丅扨弮暯嬒偩偲丄乽乮0.6亄1乯亐2乿偲偄偆寁嶼偱0.8偵側傝傑偡丅
偲偙傠偑丄攦偄暔偐偛偺寁嶼偱偼丄崌寁戙嬥偼婎弨帪揰400墌丄斾妑帪揰360墌偵側傝傑偡丅
崌寁戙嬥偺曄壔攞棪偼0.9攞偱偡丅暔壙巜悢偼100仺90偱0.9攞偵側偭偨偺偱偡丅
偙偺崌寁戙嬥偺寁嶼丄偮傑傝暔壙巜悢偺寁嶼偑乽壛廳暯嬒乿偵側偭偰偄傞偺偱偡丅
丂婎弨帪揰偱尒傞偲丄峸擖戙嬥偼儈僇儞傛傝儕儞僑偺曽偑3攞戝偒偄丅
偦傟傪斀塮偝偣偰暯嬒偡傞偺偑乽壛廳暯嬒側偺偱偡乿丅壛廳暯嬒偼丄廳傒傪斀塮偝偣偨暯嬒丅
偙偺応崌偼丄儈僇儞100墌丄儕儞僑300墌偲偄偆婎弨帪揰偺戙嬥傪廳傒偵偟偰丄壛廳暯嬒偟偰偄傑偡丅
廳傒偵偡傞悢帤傪乽僂僄僀僩乿偲屇傃傑偡丅
婎弨帪壛廳憡懳朄嶼幃傗斾妑帪壛廳憡懳朄嶼幃偺乽壛廳乿偼丄僂僄僀僩偺堄枴偱巊傢傟偰偄傑偡丅
乽儘僂巜悢乿乽僂僄僀僩嶲徠帪壛廳憡懳朄嶼幃乿傪峫偊傞
丂暔壙巜悢偺寁嶼曽幃偺愢柧傪懕偗偰偒傑偟偨丅
昅幰偼丄偙偺曽柺偺曌嫮傪偟偰丄19悽婭慜敿偵妶桇偟偨塸崙偺妛幰丄儘僂巵偑執戝偩偭偨偲巚偄傑偟偨丅
丂儘僂巵偼丄攦偄暔偐偛偺宍偱壛廳暯嬒偡傞曽幃傪採彞丅儘僂巜悢偲傕尵傢傟傑偡丅
儔僗僷僀儗僗巜悢傗僷乕僔僃巜悢偺曣懱偲側傞傕偺偱偡丅
儘僂巜悢傕丄婎弨帪揰偲斾妑帪揰偺攦偄暔偐偛崌寁戙嬥傪斾妑偟傑偡丅
儔僗僷僀儗僗巜悢傗僷乕僔僃巜悢偲偺堘偄偼丄奺昳栚偺悢検傪偄偮偺帪揰偱屌掕偡傞偐偱偡丅
儘僂巜悢偱偼乽悢検傪屌掕偡傞帪揰偼偄偮偱傕偄偄乿偲偝傟傑偟偨丅
婎弨帪揰偑2015擭丄斾妑帪揰偑2018擭偩偲偟傑偟傚偆丅
儘僂巜悢偱偼丄悢検傪屌掕偡傞帪揰偼丄2010擭偱傕2011擭偱傕2017擭偱傕偄偄偙偲偵側傝傑偡丅
丂暔壙巜悢偺悽奅偱偼丄悢検傪屌掕偡傞帪揰偼乽僂僄僀僩嶲徠帪揰乿偲屇偽傟傑偡丅
暦偒側傟側偄尵梩偱嫲弅偱偡偑丄偙偙偱傕偦偺尵梩傪巊偄傑偡丅
婎弨帪揰傪100偲偟偨斾妑帪揰偺暔壙巜悢偺寁嶼幃偼丄儘僂巜悢偱偼師偺捠傝偱偡丅

丂偙偺幃偺乽僂僄僀僩嶲徠帪揰乿偺偲偙傠傪乽婎弨帪揰乿傗乽斾妑帪揰乿偵抲偒姺偊偰偔偩偝偄丅
婎弨帪揰偵抲偒姺偊傞偲丄儔僗僷僀儗僗巜悢偺寁嶼幃偵側偭偰偄傑偡丅
斾妑帪揰偵抲偒姺偊偨応崌偼丄僷乕僔僃巜悢偺寁嶼幃偵曄傢傝傑偡丅
悢検傪屌掕偡傞帪揰傪婎弨帪揰偵偟偨儘僂巜悢偑儔僗僷僀儗僗巜悢偱偁傝丄
悢検傪屌掕偡傞帪揰傪斾妑帪揰偵偟偨儘僂巜悢偑僷乕僔僃巜悢偱偡丅
儘僂巜悢偺拞偺摿庩側働乕僗偑丄儔僗僷僀儗僗巜悢傗僷乕僔僃巜悢側偺偱偡
丂儘僂巜悢丄儔僗僷僀儗僗巜悢丄僷乕僔僃巜悢偺娭學傪妛傫偱昅幰偑敪尒偟偨帠幚偑偁傝傑偡丅
儘僂巜悢偼悢検傪巊偭偰寁嶼偟傑偡丅
偦傟偵懳墳偡傞宍偱悢検傪巊傢側偄乽僂僄僀僩嶲徠帪壛廳憡懳朄嶼幃乿偲偄偆寁嶼曽朄偑峫偊傜傟傑偡丅
乽僂僄僀僩嶲徠帪壛廳憡懳朄嶼幃乿偼昅幰偺憿岅偱偡丅師偺傛偆偵寁嶼偟傑偡丅
丂偁傞昳栚偺亊亊帪揰偺戙嬥偼丄偦偺昳栚偺僂僄僀僩嶲徠帪揰偺戙嬥偵丄
乽亊亊帪揰偺扨壙偼僂僄僀僩嶲徠帪揰偺扨壙偺壗攞偐乿偺曄壔攞棪傪妡偗偨悢帤偵側傝傑偡丅
亊亊帪揰偑婎弨帪揰傗斾妑帪揰偺応崌偼丄亊亊帪揰偺晹暘傪婎弨帪揰傗斾妑帪揰偵抲偒姺偊傟偽偄偄丅
丂偙偺傛偆側庤弴偱丄攦偄暔偐偛偺斾妑帪揰偺崌寁戙嬥傗婎弨帪揰偺崌寁戙嬥傪弌偡丅
偦偟偰丄斾妑帪偺崌寁戙嬥傪婎弨帪偺崌寁戙嬥偱妱偭偰丄100傪妡偗傑偡丅
偙傟偵傛偭偰丄僂僄僀僩嶲徠帪壛廳憡懳朄嶼幃偺寁嶼幃偵側傝傑偡丅妋擣偟偰偔偩偝偄丅

丂偙偺寁嶼幃偺拞偺僂僄僀僩嶲徠帪揰傪婎弨帪揰偵抲偒姺偊偰傒偰偔偩偝偄丅
僂僄僀僩嶲徠帪壛廳憡懳朄嶼幃偼丄婎弨帪壛廳憡懳朄嶼幃偵曄傢傝傑偡丅
僂僄僀僩嶲徠帪揰傪斾妑帪揰偵抲偒姺偊偨応崌偼丄斾妑帪壛廳憡懳朄嶼幃偵曄傢傝傑偡丅
丂僂僄僀僩嶲徠帪壛廳憡懳朄嶼幃偺拞偺摿庩側働乕僗偑丄婎弨帪壛廳憡懳朄嶼幃傗斾妑帪壛廳憡懳朄嶼幃側偺偱偡丅
娙扨偵偮偐傔傞屄暿昳栚偺塭嬁搙
丂暔壙巜悢偺寁嶼偱偼丄暔壙巜悢曄壔棪傊偺奺昳栚偺塭嬁搙偑柧妋偵偮偐傔傑偡丅
寁嶼偺巇慻傒偑攦偄暔偐偛僗僞僀儖偩偐傜偱偡丅
偙傟偼嬌傔偰廳梫側億僀儞僩側偺偱丄偟偭偐傝妛傫偱偔偩偝偄丅
丂攦偄暔偐偛偺恾傪尒偰偔偩偝偄丅偐偛偵偼3昳栚偩偗偑擖偭偰偄傑偡丅
昳栚嘆偺戙嬥偼乽俙墌仺俙丩墌乿丄昳栚嘇偺戙嬥偼乽俛墌仺俛丩墌乿丄
昳栚嘊偺戙嬥偼乽俠墌仺俠丩墌乿偲悇堏偟偨偲壖掕偟傑偡丅
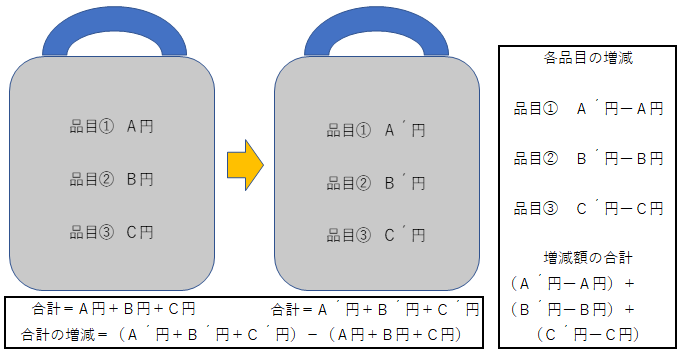
丂攦偄暔偐偛崌寁戙嬥偼乽俙墌亄俛墌亄俠墌乿偐傜乽俙丩墌亄俛丩墌亄俠丩墌乿偵曄傢傝傑偟偨丅
崌寁戙嬥偺憹尭妟偼乽乮俙丩墌亄俛丩墌亄俠丩墌乯乕乮俙墌亄俛墌亄俠墌乯乿偱偡丅
曄宍偡傞偲丄乽俙丩墌亄俛丩墌亄俠丩墌亅俙墌亅俛墌亅俠墌乿偱偡丅
偝傜偵曄宍偡傞偲丄乽乮俙丩墌亅俙墌乯亄乮俛丩墌亅俛墌乯亄乮俠丩墌亅俠墌乯乿偵側傝傑偡丅
丂師偵恾偺塃懁偺奺昳栚偺憹尭妟傪尒偰偔偩偝偄丅
昳栚嘆偼乮俙丩墌亅俙墌乯丄昳栚嘇偼乮俛丩墌亅俛墌乯丄昳栚嘊偼乮俠丩墌乕俠墌乯偱偡丅
奺昳栚偺憹尭妟偺崌寁偼乽乮俙丩墌亅俙墌乯亄乮俛丩墌亅俛墌乯亄乮俠丩墌亅俠墌乯乿偵側傝傑偡丅
丂偙傟偼丄崌寁戙嬥偺憹尭妟偺幃傪曄宍偝偣偨幃偲傑偭偨偔摨偠偱偡丅
偮傑傝丄攦偄暔偐偛崌寁戙嬥偺憹尭妟偼丄奺昳栚偺憹尭妟偺崌寁偲摨偠偵側傞偺偱偡丅
攦偄暔偐偛崌寁戙嬥偺曄壔棪偼丄暔壙巜悢偺曄壔棪偲僀僐乕儖偱偡丅
廬偭偰丄暔壙巜悢曄壔棪傊偺奺昳栚偺塭嬁搙偑偮偐傔傞傢偗偱偡丅
丂偙偆偄偭偨嵎偟堷偒寁嶼偼丄擔忢偺攦偄暔偱傕堄幆偟偰偄傞恖偑懡偄偱偟傚偆丅
慜寧偲崱寧偺奺昳栚傊偺巟弌嬥妟傪妋擣偟偰傒偨俙偝傫偺椺傪弌偟傑偟傚偆丅
乽暷戙偼500墌尭偭偨丅栰嵷戙偼300墌憹偊偨丅僈僜儕儞戙傕200墌憹偊偨丅嵎偟堷偒偡傞偲亇僛儘偱偡偹乿丅
擄偟偦偆側乽婑梌搙乿偺寁嶼傕幚偼娙扨柧椖
丂暔壙巜悢偺悽奅偱偼丄暔壙巜悢曄壔棪傊偺奺昳栚偺塭嬁搙偼乽婑梌搙乿偲偟偰偒偭偪傝寁嶼偟傑偡丅
儈僇儞丄儕儞僑丄僶僫僫偑擖偭偨壥暔偐偛儌僨儖偱峫偊傑偡丅恾傪尒偰偔偩偝偄丅
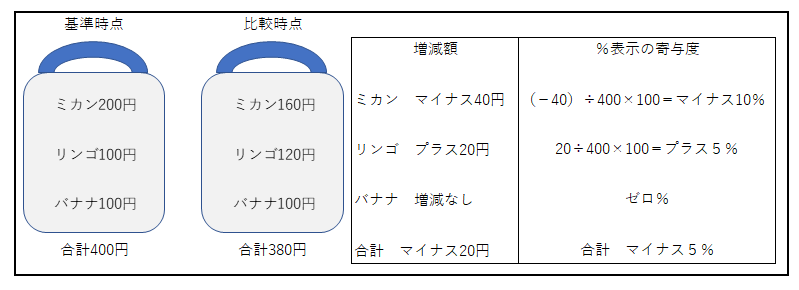
丂攦偄暔偐偛崌寁戙嬥偺憹尭偼丄婎弨帪揰400墌仺斾妑帪揰380墌側偺偱丄儅僀僫僗20墌丅
尭彮棪偼丄偙偺儅僀僫僗20墌傪婎弨帪揰偺崌寁戙嬥偺400墌偱妱傟偽弌傑偡丅
乽儅僀僫僗20墌亐400墌乿偲偄偆寁嶼偱丄儅僀僫僗0.05偲側傝傑偡丅
亾昞帵偵偡傞偵偼100傪妡偗傑偡丅儅僀僫僗5亾偱偡丅偙傟偑崌寁戙嬥偺曄壔棪丅
攦偄暔偐偛崌寁戙嬥偺曄壔棪僀僐乕儖暔壙巜悢曄壔棪側偺偱丄暔壙巜悢曄壔棪偼儅僀僫僗5亾偱偡丅
暔壙巜悢偼乽100仺95乿偺悇堏側偺偱丄壓棊棪偼娫堘偄側偔5亾偱偡丅
丂奺昳栚偺婑梌搙傕摨偠傛偆偵寁嶼偟傑偡丅儈僇儞戙嬥偺憹尭偼儅僀僫僗40墌丅
偙傟傪婎弨帪揰偺崌寁戙嬥偺400墌偱妱傟偽丄婑梌搙偑儅僀僫僗0.1偲弌傑偡丅
亾昞帵偱偼丄100傪妡偗偨儅僀僫僗10亾偱偡丅
丂儕儞僑戙嬥偺憹尭偼僾儔僗20墌丅偙傟傪婎弨帪揰偺崌寁戙嬥偺400墌偱妱傝傑偡丅
婑梌搙偼僾儔僗0.05丅亾昞帵偵偡傞偨傔偵100傪妡偗偰丄亾昞帵偺婑梌搙偼5亾偲側傝傑偡丅
僶僫僫偼戙嬥偺憹尭偼側偄偺偱丄婑梌搙偼僛儘亾偱偡丅
丂惍棟偡傞偲丄亾昞帵偺婑梌搙偼乽儈僇儞偑儅僀僫僗10亾丄儕儞僑偑僾儔僗5亾丄僶僫僫偑0亾乿偱偡丅
婑梌搙偺崌寁偼儅僀僫僗5亾偱偡丅偙傟偼攦偄暔偐偛崌寁戙嬥偺曄壔棪偲摨偠丅
攦偄暔偐偛崌寁戙嬥偺曄壔棪僀僐乕儖暔壙巜悢曄壔棪側偺偱丄
奺昳栚偺婑梌搙偺崌寁偼丄暔壙巜悢曄壔棪偲傕堦抳偟傑偡丅偙傟偼忢偵惉傝棫偮摍幃偱偡丅
寁嶼幃傪恾帵偟偰偍偒傑偡偺偱丄偟偭偐傝妎偊偰偔偩偝偄丅

丂暔壙巜悢偺寁嶼偱丄奺昳栚偺婑梌搙偑偒偭偪傝寁嶼偱偒傞偙偲偺儊儕僢僩偼戝偒偄偱偡丅
暔壙巜悢偺曄壔偵偮偄偰偺愢柧偱丄奺昳栚偺塭嬁嬶崌傪惓妋偵揱偊傜傟傑偡丅
丂岤楯徣偵傛傞暔壙婾憰偺僇儔僋儕偺尋媶偵傕丄婑梌搙偺暘愅偑戝偒側晲婍偵側傝傑偡丅
僩僢僾儁乕僕偵栠傞








































